The situation is depicted in the figure below.

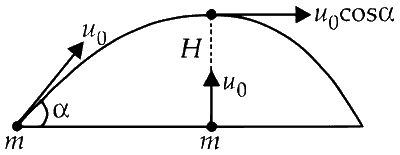
At the highest point of the first particle’s trajectory, its speed is given by :

$ \text{Speed of the first particle} = u_0 \cos \alpha $

For the second particle, which was thrown vertically upward, the speed at its highest point is calculated as :

$ \text{Speed of the second particle} = \sqrt{u_0^2 - 2gH} $

Where $ H $ is the maximum height reached by the second particle :

$ H = \frac{u_0^2 \sin^2 \alpha}{2g} $

Therefore, the speed of the second particle at the highest point becomes :

$ = \sqrt{u_0^2 - \frac{2g \left( u_0^2 \sin^2 \alpha \right)}{2g}} = \sqrt{u_0^2 - u_0^2 \sin^2 \alpha} = u_0 \cos \alpha $

Thus, at the highest point :

According to the law of conservation of linear momentum in the horizontal direction :

$ mu_0 \cos \alpha = 2mv_1 $

$ \implies v_1 = \frac{u_0 \cos \alpha}{2} \quad \text{... (i)} $

In the vertical direction :

$ mu_0 \cos \alpha = 2mv_2 $

$ \implies v_2 = \frac{u_0 \cos \alpha}{2} \quad \text{... (ii)} $

Let $ \theta $ be the angle that the composite system makes with the horizontal immediately after the collision. Then :

$ \tan \theta = \frac{v_2}{v_1} = 1 \quad \text{(Using (i) and (ii))} $

$ \therefore \theta = \tan^{-1} 1 = 45^\circ = \frac{\pi}{4} $