The speed of light in a medium is given by the equation :

$$ \frac{C}{V}=\frac{\lambda_0}{\lambda}=\mu $$

Where :

• V is the velocity of light in the medium
• λ is the wavelength of light in the medium
• λ₀ is the wavelength in free space
• μ is the refractive index of the medium

Given :

$$ \lambda=\frac{2}{3} \lambda_0 $$

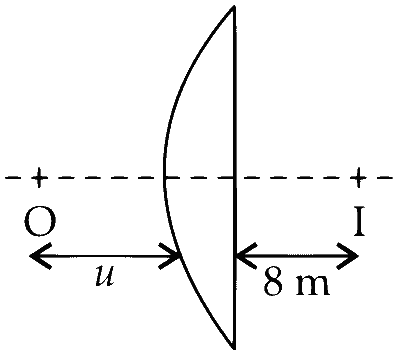
Using the given data :

$$\begin{aligned} u & = -24 \text{ m},\\\\ h_i & = \frac{1}{3}h_0\end{aligned}$$

To find the magnification (m) :

$$ m = \frac{h_i}{h_0} = \frac{1}{3} = \frac{v}{u} $$

Hence,

$$ v = \frac{u}{3} $$

Given :

$$ v = 8 \text{ m},\ u = -24 \text{ m} $$

Applying the lens formula :

$$ \frac{1}{v} - \frac{1}{u} = \frac{1}{f} = (\mu - 1)\left(\frac{1}{R_1} - \frac{1}{R_2}\right) $$

Since the plane surface has an infinite radius :

$$ \frac{1}{\infty} = 0 $$

Therefore :

$$\frac{1}{8} - \frac{1}{-24} = (1.5 - 1)\left(\frac{1}{R} - 0\right)$$

$$\Rightarrow \frac{1}{6} = \frac{0.5}{R}$$

Solving for R :

$$ \Rightarrow R = 3 \text{ m} $$