The situation is as shown in the figure.

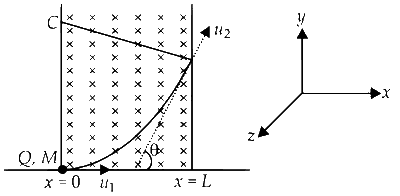
Here, $${\overrightarrow u _1} = 4\widehat i$$ ms^$$-$$1

$${\overrightarrow u _2} = 2\left( {\sqrt 3 \widehat i + \widehat j} \right)$$ ms^$$-$$1

When the charged particle enters in an uniform magnetic field, it travels a circular path.

Component of final velocity of particle is in positive y direction.

Centre of circle is present on positive y-axis.

So, magnetic field is present in negative z-direction.

Angle of deviation

$$\tan \theta = {{{u_{2y}}} \over {{u_{2x}}}} = {2 \over {2\sqrt 3 }} = {1 \over {\sqrt 3 }}$$

$$\theta = {\tan ^{ - 1}}\left( {{1 \over {\sqrt 3 }}} \right) = 30^\circ = {\pi \over 6}$$

$$\omega = {\theta \over t}$$

$$\therefore$$ $$t = {\theta \over \omega } = {\theta \over {(QB/M)}} = {{M\theta } \over {QB}}$$ ($$\because$$ $$\omega = {{QB} \over M}$$

$$\therefore$$ $$B = {{M\theta } \over {Qt}} = {{M\pi } \over {6Q \times 10 \times {{10}^{ - 3}}}}$$ (.... t = 10 ms = 10^$$-$$3 s)

$$ = {{100\pi M} \over {6Q}} = {{50\pi M} \over {3Q}}$$