JEE Advance - Physics (2013 - Paper 1 Offline - No. 17)
A horizontal stretched string, fixed at two ends, is vibrating in its fifth harmonic according to the equation
y(x, t) = (0.01 m) sin[(62.8 m$$-$$1)x] cos[(628 s$$-$$1)t]
Assuming $$\pi$$ = 3.14, the correct statement(s) is(are)
The number of nodes is 5.
The length of the string is 0.25 m.
The maximum displacement of the mid-point of the string, from its equilibrium position is 0.01 m.
The fundamental frequency is 100 Hz.
Explanation
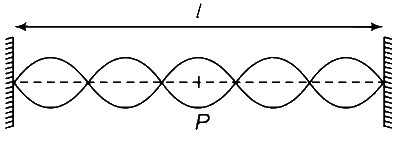
Number of nodes = 6
From the given equation, we can see that
$$k = {{2\pi } \over \lambda } = 62.8$$ m$$-$$1
$$\therefore$$ $$\lambda = {{2\pi } \over {62.8}}$$ m = 0.1 m
$$1 = {{5\lambda } \over 2}$$ = 0.25 m
The mid-point of the string is P, an antinode
$$\therefore$$ maximum displacement = 0.01 m
$$\omega$$ = 2$$\pi$$f = 628 s$$-$$1
$$\therefore$$ $$f = {{628} \over {2\pi }} = 100$$ Hz
But this is fifth harmonic frequency.
$$\therefore$$ Fundamental frequency f0
$$ = {f \over 5} = 20$$ Hz.
Comments (0)


