Consider the disc and the rings together as a system. Since the external torque $\vec{\Gamma}_{\text {ext }}$ is zero, the angular momentum of the system about the vertical axis through $O$ is conserved, which can be expressed as:

$$ I_i \omega_i = I_f \omega_f $$

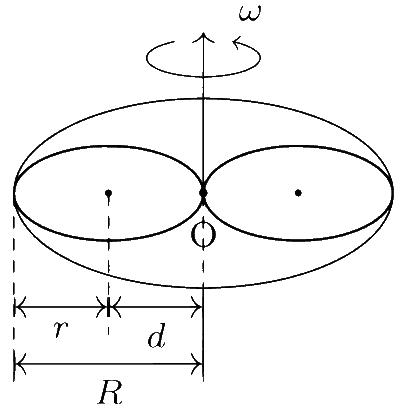
Initially, the moment of inertia is due to the disc alone, and its value is:

$$ I_i = \frac{1}{2} M R^2 = \frac{1}{2} \times 50 \times 0.4^2 = 4 \mathrm{~kg \cdot m}^2 $$

The moment of inertia of a ring with mass $m$ and radius $r$ about an axis perpendicular to its center is $m r^2$. Using the theorem of parallel axes, the ring's moment of inertia about the axis of rotation is given by:

$$ I_{\text{ring}} = m r^2 + m d^2 = 2 m r^2 $$

where $d = r$ is the distance between the parallel axes. Thus, the moment of inertia of the complete system in the final configuration is:

$$ \begin{aligned} I_f &= \frac{1}{2} M R^2 + 2 m r^2 + 2 m r^2 \\ &= \frac{1}{2} (50)(0.4)^2 + 2 \left(2(6.25)(0.2)^2\right) = 5 \mathrm{~kg \cdot m}^2 \end{aligned} $$

With no external torque acting on the system, the angular momentum is conserved:

$$ \begin{aligned} I_i \omega_i &= I_f \omega_f \\ 4 \times 10 &= 5 \omega_f \\ \omega_f &= 8 \mathrm{~rad/s} \end{aligned} $$