Since Cylinder P has most of its mass concentrated near its surface, its moment of inertia (about the cylinder axis) is greater than that of Cylinder Q, i.e., $ I_P > I_Q $. The forces acting on the cylinder include its weight $ mg $, the normal reaction $ N $, and the frictional force $ f $.

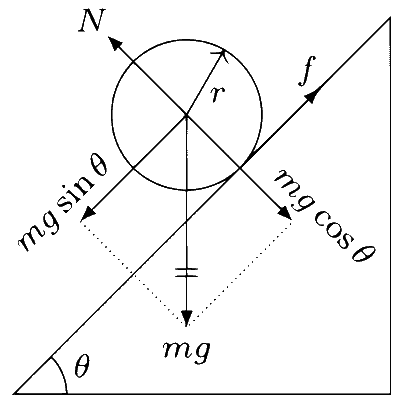
In the case of rolling without slipping, we have :

$ v = \omega r $

$ a = \alpha r $

The torque about the center of mass is related to $\alpha$ by :

$ \tau = rf = I\alpha \quad (1) $

The force along the plane is related to $a$ by :

$ mg \sin \theta - f = ma \quad (2) $

By solving equations (1) and (2), we get :

$ a = \frac{g \sin \theta}{1 + \frac{I}{mr^2}} \quad (3) $

From equation (3), it follows that $ a_P < a_Q $ (since $ I_P > I_Q $). Therefore, Cylinder P reaches the ground later, has a lower velocity, lower angular velocity ($\omega = \frac{v}{r}$), and lower translational kinetic energy.

For verification, the conservation of energy can be used :

$ mgh = \frac{1}{2}mv^2 + \frac{1}{2}I\omega^2 $

This yields :

$ \frac{1}{2}mv_P^2 < \frac{1}{2}mv_Q^2 $

Thus :

$ v_P < v_Q, \ \omega_P < \omega_Q, \ a_P < a_Q $

And the time relationships :

$ t_P > t_Q $