Sign In

JEE Advance - Physics (2012 - Paper 2 Offline - No. 8)

The figure shows a system consisting of (i) a ring of outer radius 3R rolling clockwise without slipping on a horizontal surface with angular speed $$\omega $$ and (ii) an inner disc of radius 2R rotating anti-clockwise with angular speed $${\omega \over 2}$$. The ring and disc are separated by frictionless ball bearings. The point P on the inner disc is at a distance R from the origin, where OP makes an angle of $$30^\circ $$ with the horizontal. Then with respect to the horizontal surface,
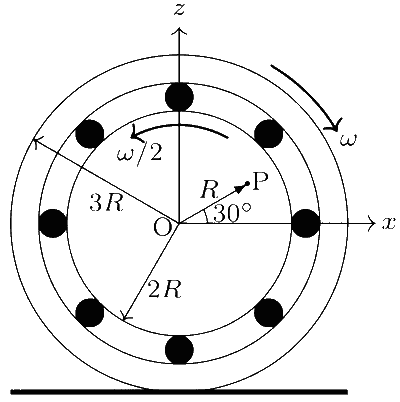
IIT-JEE 2012 Paper 2 Offline Physics - Rotational Motion Question 54 English
the point O has linear velocity $$3R\omega \widehat i$$
the point P has linear velocity $${{11} \over 4}R\omega \widehat i + {{\sqrt 3 } \over 4}R\omega \widehat k$$
the point P has linear velocity $${{13} \over 4}R\omega \widehat i - {{\sqrt 3 } \over 4}R\omega \widehat k$$
the point P has linear velocity $$\left( {3 - {{\sqrt 3 } \over 4}} \right)R\omega \widehat i + {1 \over 4}R\omega \widehat k$$

Explanation

The outer ring rolls without slipping, meaning the point on the ring in contact with the ground (denoted as point C) is stationary, i.e., $ \vec{v}_{\mathrm{C}} = \overrightarrow{0} $. Therefore, the velocity of point O is :

$$ \vec{v}_{\mathrm{O}} = \vec{v}_{\mathrm{C}} + \vec{\omega}_{\mathrm{o}} \times \vec{r}_{\mathrm{CO}} = \overrightarrow{0} + \omega \hat{\jmath} \times 3R \hat{k} = 3R\omega \hat{\imath} $$

Point P is located on the inner disc, which has an angular velocity $ \vec{\omega}_{\mathrm{i}} = -\omega / 2 \hat{\jmath} $. The position vector from O to P is given by :

$$ \vec{r}_{\mathrm{OP}} = R \cos 30^{\circ} \hat{\imath} + R \sin 30^{\circ} \hat{k} = \frac{\sqrt{3} R}{2} \hat{\imath} + \frac{R}{2} \hat{k} $$

Thus, the velocity of point P is calculated as follows :

$$ \begin{aligned} \vec{v}_{\mathrm{P}} & = \vec{v}_{\mathrm{O}} + \vec{\omega}_{\mathrm{i}} \times \vec{r}_{\mathrm{OP}} \\ & = 3R\omega \hat{\imath} + \left(-\frac{\omega}{2} \hat{\jmath}\right) \times \left(\frac{\sqrt{3} R}{2} \hat{\imath} + \frac{R}{2} \hat{k}\right) \\ & = \frac{11\omega R}{4} \hat{\imath} + \frac{\sqrt{3} \omega R}{4} \hat{k} . \end{aligned} $$

Comments (0)

Advertisement