Consider a thin, uniform cylindrical shell that is closed at both ends and partially filled with water. This cylindrical shell is floating vertically in water, with exactly half of its height submerged. The relative density of the shell's material compared to water is denoted by $${\rho_c}$$.

The inner radius of the cylindrical shell is $r_1$, the outer radius is $r_2$, the height is $h$, and the material density is $\rho$. The shell is filled with water, which has a density of $\rho_w$, up to a height of $x$. Given $${\rho_c = \frac{\rho}{\rho_w}}$$, we know that the cylinder is in a half-submerged state, meaning $h/2$ of the cylinder's height is submerged in water.

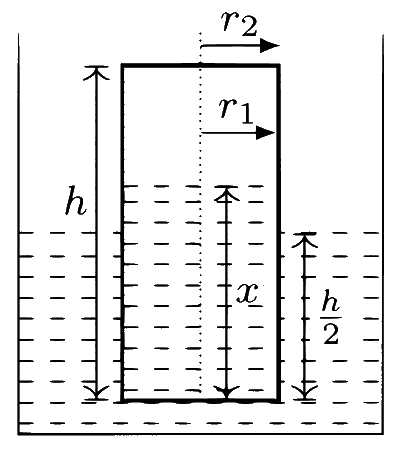
In equilibrium, the weight of the cylindrical shell, including the water inside it, must equal the buoyant force (upthrust) acting on it. This relationship can be expressed as follows:

$$ \left(\pi r_2^2-\pi r_1^2\right) h \rho g + \pi r_1^2 x \rho_w g = \pi r_2^2\left(\frac{h}{2}\right)\rho_w g $$

By simplifying this equation, we get:

$$ x = h\left[\frac{r_2^2}{r_1^2}\left(0.5-\rho_c\right)+\rho_c\right] = h\left[0.5+\frac{r_2^2-r_1^2}{r_1^2}\left(0.5-\rho_c\right)\right] ...........(i) $$

From equation (i), we can determine the condition under which $x$ is greater than $0.5h$. This occurs if $\rho_c < 0.5\left(\because r_2 > r_1\right)$.