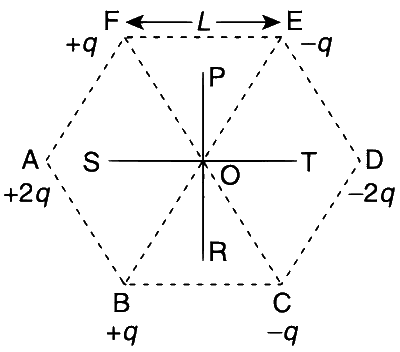
The electric field at point $O$ due to the charges at vertices $A$ and $D$ is $4K$ along the direction OD. Similarly, due to the charges at vertices $B$ and $E$, the electric field is $2K$ along the direction OE, and due to the charges at vertices $C$ and $F$, it is $2K$ along the direction OC. Given the uniform geometry of this setup, the resulting electric field is $6K$ along OD.

The potential at point $O$ is calculated as :

$$ V_{\mathrm{O}}=\sum \frac{1}{4 \pi \epsilon_0} \frac{q_i}{L} = \frac{1}{4 \pi \epsilon_0 L} \sum q_i = 0 $$

For any point on the line PR, we observe that there are pairs of equal and opposite charges equidistant from these points, making the potential at any point on PR zero. If we consider points on OS, the potential is positive, while for points on OT, the potential is negative. The potential at points on the line ST, at a distance $x$ from $O$ (with $x$ considered positive towards the right), can be shown to be :

$$ \begin{aligned} V(x) = \frac{q}{4 \pi \epsilon_0} \left[ \frac{2}{\sqrt{L^2 + x^2 + xL}} - \frac{2}{\sqrt{L^2 + x^2 - xL}} - \frac{4x}{L^2 - x^2} \right]. \end{aligned} $$