JEE Advance - Physics (2012 - Paper 2 Offline - No. 19)
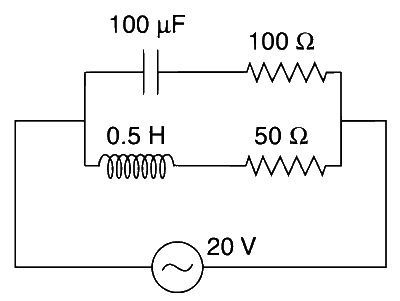
In the given circuit, the AC source has $$\omega$$ = 100 rad/s. Considering the inductor and capacitor to be ideal, the correct choice(s) is(are)
Explanation
Here, $$\Omega$$ = 100 rad/s, L = 0.5 H, C = 100 $$\mu$$F, V = 20 V
$$\therefore$$ $${X_L} = \omega L = 100 \times 0.5 = 50\,\Omega $$
$${X_C} = {1 \over {\omega C}} = {1 \over {100 \times 100 \times {{10}^{ - 6}}}} = 100\,\Omega $$
Impedance across capacitor,
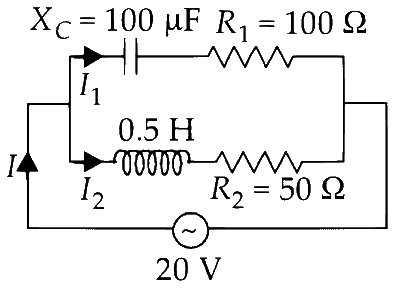
$${Z_1} = \sqrt {{R^2} + X_C^2} $$
$$ = \sqrt {{{(100)}^2} + {{(100)}^2}} $$
$${Z_1} = 100\sqrt 2 \,\Omega $$
$$\therefore$$ $${I_1} = {{20} \over {100\sqrt 2 }} = {1 \over {5\sqrt 2 }}\,A$$
Voltage across 100 $$\Omega$$
$$V = {I_1} \times 100 = {1 \over {5\sqrt 2 }} \times 100 = 10\sqrt 2 \,V$$
Impedance across inductance,
$${Z_2} = \sqrt {{R^2} + {{({X_L})}^2}} = \sqrt {{{(50)}^2} + {{(50)}^2}} $$
$${Z_2} = 50\sqrt 2 \,\Omega $$
$$\therefore$$ $${I_2} = {{20} \over {50\sqrt 2 }} = {2 \over {5\sqrt 2 }} = {{\sqrt 2 } \over 5}$$
Now, voltage across $$50\,\Omega = {{\sqrt 2 } \over 5} \times 50 = 10\sqrt 2 $$
$${I_1} = {1 \over {5\sqrt 2 }}A$$ at 45$$^\circ$$ leading
$${I_2} = {{\sqrt 2 } \over 5}A$$ at 45$$^\circ$$ lagging
$$\therefore$$ Current through circuit
$${I_{net}} = \sqrt {I_1^2 + I_2^2} = \sqrt {{{\left( {{1 \over {5\sqrt 2 }}} \right)}^2} + \left( {{{\sqrt 2 } \over 5}} \right)} = 0.3\,A$$
Comments (0)


