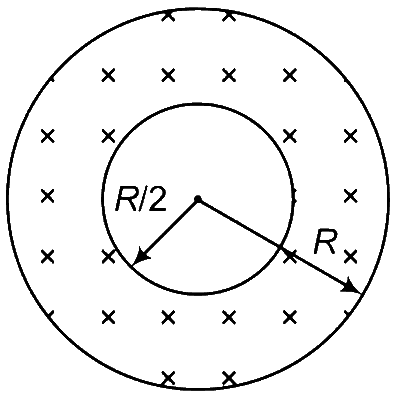
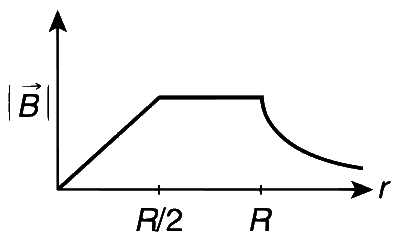
r = distance of a point from centre.

For r $$\le$$ R/2 Using Ampere's circuital law,

$$\oint {B.\,dl} $$

or, $$Bl = {\mu _0}({I_{in}})$$

$$B(2\pi r) = {\mu _0}({I_{in}})$$

$$B = {{{\mu _0}} \over {2\pi }}{{{I_{in}}} \over r}$$ ...... (i)

Since, $${I_{in}} = 0$$ $$\therefore$$ $$B = 0$$

For $${R \over 2} \le r \le R$$

$${I_{in}} = \left[ {\pi {r^2} - \pi {{\left( {{R \over 2}} \right)}^2}} \right]\sigma $$

Here $$\sigma$$ = current per unit area.

Substituting in Eq. (i), we have

$$B = {{{\mu _0}} \over {2\pi }}{{\left[ {\pi {r^2} - \pi {{{R^2}} \over 2}} \right]\sigma } \over r}$$

$$ = {{{\mu _0}\sigma } \over {2r}}\left( {{r^2} - {{{R^2}} \over 4}} \right)$$

At $$r = {R \over 2},\,B = 0$$

At $$r = R,\,B = {{3{\mu _0}\sigma R} \over 8}$$

For r $$\ge$$ R

$${I_{in}} = {I_{Total}} = I$$ (say)

Therefore, substituting in Eq. (i), we have

$$B = {{{\mu _0}} \over {2\pi }}.\,{I \over r}$$

or, $$B \propto {1 \over r}$$