JEE Advance - Physics (2012 - Paper 2 Offline - No. 11)
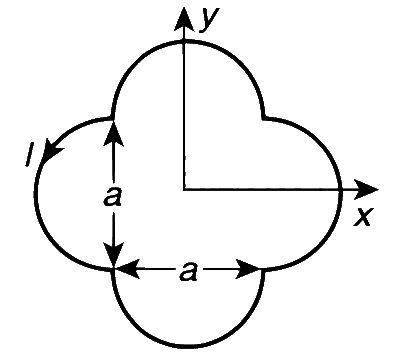
A loop carrying current $$l$$ lies in the xy-plane as shown in the figure. The unit vector $$\widehat k$$ is coming out of the plane of the paper. The magnetic moment of the current loop is
$${a^2}I\widehat k$$
$$\left( {{\pi \over 2} + 1} \right){a^2}I\widehat k$$
$$ - \left( {{\pi \over 2} + 1} \right){a^2}I\widehat k$$
$$(2\pi + 1){a^2}I\widehat k$$
Explanation
Area of the loop
$$A = \left[ {{a^2} + 4 \times {{\pi {{\left( {{a \over 2}} \right)}^2}} \over 2}} \right]\widehat k = \left[ {{a^2} + {{\pi {a^2}} \over 2}} \right]\widehat k$$
Therefore, the magnetic moment of the current loop is
$$M = I \times A = I\left[ {{a^2} + {{\pi {a^2}} \over 2}} \right]\widehat k = \left[ {1 + {\pi \over 2}} \right]I{a^2}\widehat k$$
Comments (0)


