JEE Advance - Physics (2012 - Paper 2 Offline - No. 10)
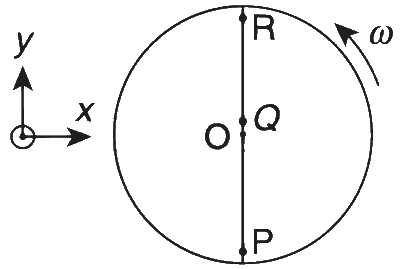
Explanation
$\left(\frac{1}{8}\right)^{\mathrm{th}}$ rotation of the disc with a constant $\Omega$ implies that the disc has turned through
$$ \frac{1}{8} \times 360^{\circ}=45^{\circ} $$
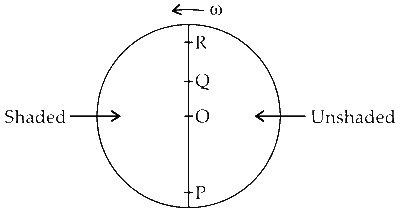
The orientation of the disc now is
For the particle thrown from $Q$ towards $R$, will have only the velocity given to it with respect to disc i.e., it possess a velocity only in the Y-Z plane and covers a range along OR. Hence, it can be seen to land on the disc in the unshaded region. Actually point $O$ of the disc has zero velocity and $Q$ being very close to $O$, will have only the velocity given to it w.r.t disc.
For the particle thrown from P , will have an additional velocity $=R \Omega$ along +X direction i.e., it will cover a range $=\frac{R}{2}$ along PO as well as a distance $=(R \omega) \frac{T}{8}=\frac{R}{8} \times 2 \pi=\frac{\pi R}{4}$ along $+X$ direction
The resultant displacement of particle P is thus obtained as
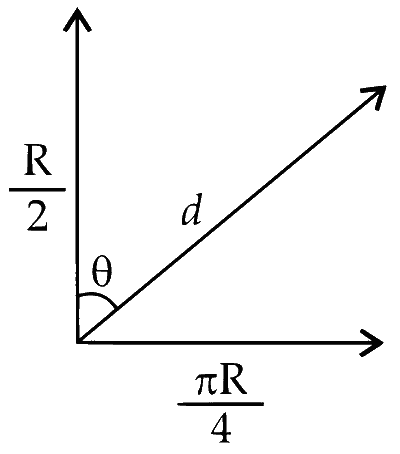
$\begin{aligned} \Rightarrow \quad d & =\frac{R}{2} \sqrt{1+\frac{\pi^2}{4}} \\ \Rightarrow \quad \pi^2 & =10 \\ d & =\frac{\mathrm{R}}{4} \sqrt{14} \\ \tan \theta & =\frac{\pi \mathrm{R} / 4}{\mathrm{R} / 2}=\frac{\pi}{2}\end{aligned}$
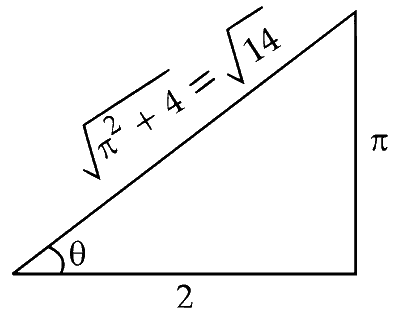
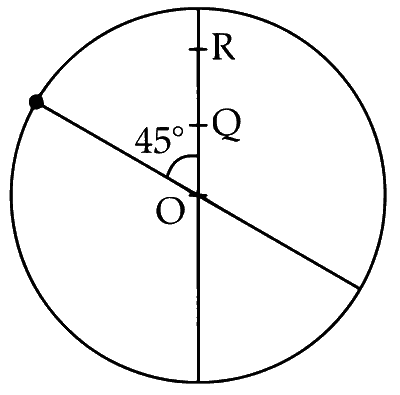
In the diagram shown,
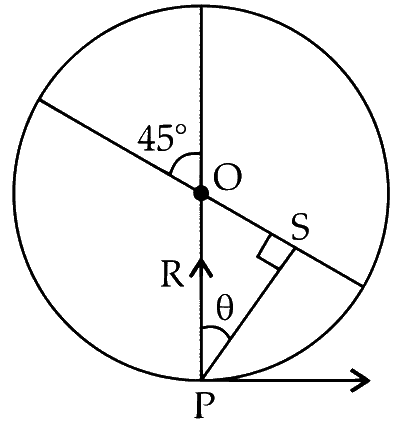
$$ \begin{aligned} P S & =R \cos \theta \\ & =R \times \frac{2}{\sqrt{14}} \\ & =\frac{2 R}{\sqrt{14}} \end{aligned} $$
Since, $d>$ PS $\quad$ PS $=\frac{R}{7} \sqrt{14}$
Hence, the particle from P also lands in the unshaded region.
Comments (0)


