JEE Advance - Physics (2012 - Paper 2 Offline - No. 1)
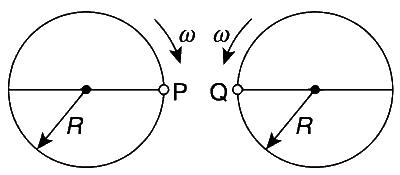
Two identical discs of same radius R are rotating about their axes in
opposite directions with the same constant angular speed $$\omega $$. The
discs are in the same horizontal plane. At time t = 0, the points P
and Q are facing each other as shown in the figure. The relative
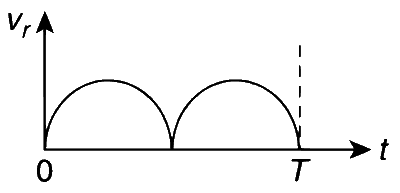
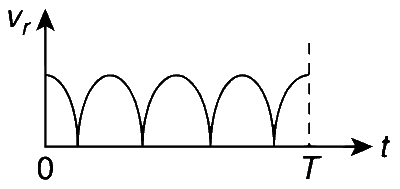
speed between the two points P and Q is vr. In one time period (T)
of rotation of the discs, vr as a function of time is best represented
by

Explanation
The relative velocity of the point $P$ w.r.t. the point $Q$ is given by
$$ \vec{v}_r=\vec{v}_P-\vec{v}_Q $$ .........(1)
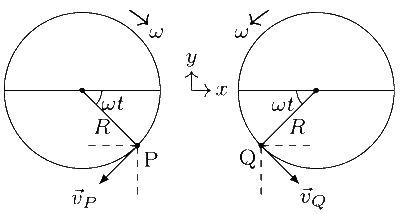
It is easy to see that $\left|\vec{v}_P\right|=\left|\vec{v}_Q\right|=\omega R$ and angle traversed in time $t$ is $\omega t$. Thus, velocities of $P$ and $Q$ are
$$ \begin{aligned} & \vec{v}_P=\omega R(-\sin \omega t \hat{\imath}-\cos \omega t \hat{\jmath}) \\ & \vec{v}_Q=\omega R(\sin \omega t \hat{\imath}-\cos \omega t \hat{\jmath}) \end{aligned} $$
Substitute $\vec{v}_P$ and $\vec{v}_Q$ in equation (1) to get $\vec{v}_r=$ $-2 \omega R \sin \omega t \hat{\imath}$ and thus $v_r=2 \omega R|\sin \omega t|$.
Comments (0)


