Sign In

JEE Advance - Physics (2012 - Paper 1 Offline - No. 9)

Three very large plates of same area are kept parallel and close to each other. They are considered as ideal black surfaces and have very high thermal conductively. The first and third plates are maintained at temperatures 2T and 3T, respectively. The temperature of the middle (i.e. second) plate under steady state condition is
$${\left( {{{65} \over 2}} \right)^{1/4}}T$$
$${\left( {{{97} \over 4}} \right)^{1/4}}T$$
$${\left( {{{97} \over 2}} \right)^{1/4}}T$$
$${(97)^{1/4}}T$$

Explanation

Let the steady state temperature of the middle plate to T0. In the steady state, the heat radiated per unit time by the middle plate is equal to the heat received per unit time by it. The middle plate radiates heat from both the surfaces and receives the heat radiated by the first and the third plates.

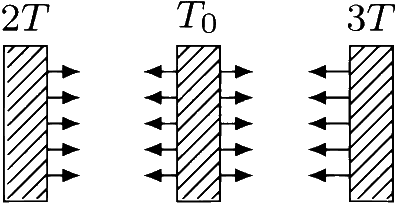
IIT-JEE 2012 Paper 1 Offline Physics - Heat and Thermodynamics Question 22 English Explanation

Stefan-Boltzmann law gives the rate of heat loss and heat gain by the middle plate as

$$d{Q_{out}}/dt = \sigma AT_0^4 + \sigma AT_0^4$$,

$$d{Q_{in}}/dt = \sigma A{(2T)^4} + \sigma A{(3T)^4}$$.

The steady state condition, $$d{Q_{out}}/dt = d{Q_{in}}/dt$$

$$\sigma A{(2T)^4} + \sigma A{(3T)^4} = \sigma 2A{({T_0})^4}$$

$$16{T^4} + 81{T^4} = 2{({T_0})^4}$$

$$97{T^4} = 2{({T_0})^4}$$

$${({T_0})^4} = {{97} \over 2}{T^4} = {\left( {{{97} \over 2}} \right)^{1/4}}T$$

Comments (0)

Advertisement