JEE Advance - Physics (2012 - Paper 1 Offline - No. 8)
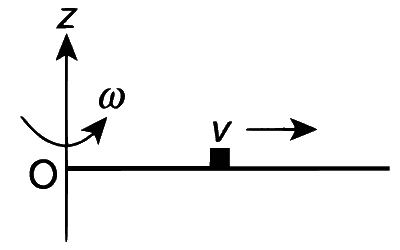
A thin uniform rod, pivoted at O, is rotating in the horizontal plane with constant angular speed $$\omega$$, as shown in the figure. At time t = 0, a small insect starts from O and moves with constant speed v, with respect to the rod towards the other end. It reaches the end of the rod at t = T and stops. The angular speed of the system remains $$\omega$$ throughout. The magnitude of the torque (|$$\tau$$|) about O, as a function of time is best represented by which plot ?
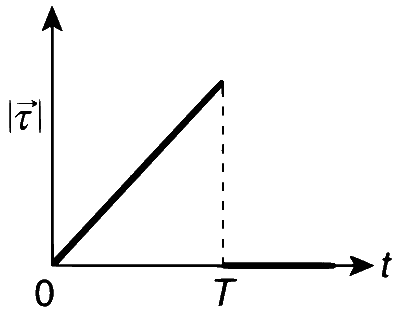
Explanation
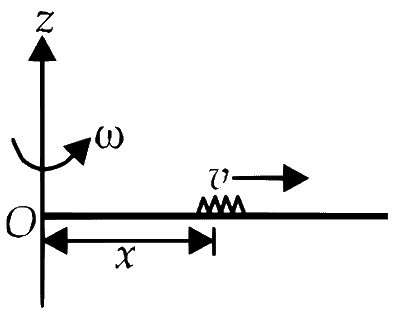
Let M and l be the mass and length of the rod respectively and m be the mass of the insect. Let the insect be at a distance x from O at any instant of time t.
$$\therefore$$ x = vt ....... (i)
Angular momentum of the system about O,
$$L = \left[ {{{M{l^2}} \over {12}} + m{x^2}} \right]\omega $$
$$ = \left[ {{{M{l^2}} \over {12}} + m{{(vt)}^2}} \right]\omega $$ (Using (i))
$$ = \left[ {{{M{l^2}} \over {12}} + m{v^2}{t^2}} \right]\omega $$
As, $$\left| {\overrightarrow \tau } \right| = {{dL} \over {dt}} = {d \over {dt}}\left[ {{{M{l^2}} \over {12}} + m{v^2}{t^2}} \right]\omega $$
As $$\omega$$ and v remain constant
$$\therefore$$ $$\left| {\overrightarrow \tau } \right| = 2m\omega {v^2}t$$
$$\left| {\overrightarrow \tau } \right| \propto t$$
Hence, the graph and t is a straight line passing through the (0, 0). Option (b) represents correct plot.
Comments (0)


