JEE Advance - Physics (2012 - Paper 1 Offline - No. 7)
A biconvex lens is formed with two planoconvex lenses as shown in the figure. Refractive index n of the first lens is 1.5 and that of the second lens is 1.2. Both curved surface are of the same radius of curvature R = 14 cm. For this biconvex lens, for an object distance of 40 cm, the image distance will be
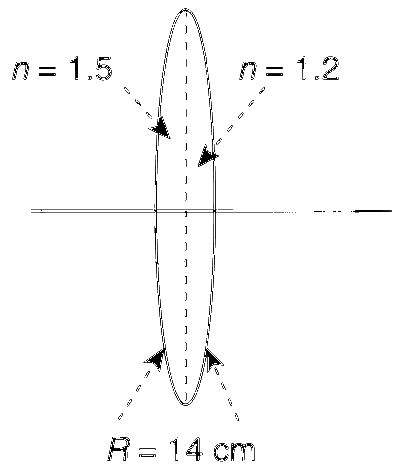
Explanation
According to lens maker's formula
$${1 \over f} = (n - 1)\left( {{1 \over {{R_1}}} - {1 \over {{R_2}}}} \right)$$
For the first lens
n = 1.5, R1 = + 14 cm, R2 = $$\infty$$
$$\therefore$$ $${1 \over {{f_1}}} = (1.5 - 1)\left( {{1 \over {14}} - {1 \over \infty }} \right) = {{0.5} \over {14}}$$
For the second lens,
n = 1.2, R1 = $$\infty$$, R2 = $$-$$14 cm
$$\therefore$$ $${1 \over {{f_2}}} = (1.2 - 1)\left( {{1 \over \infty } - {1 \over { - 14}}} \right) = {{0.2} \over {14}}$$
The focal length of the bi-convex lens is
$${1 \over f} = {1 \over {{f_1}}} + {1 \over {{f_2}}} = {{0.5} \over {14}} + {{0.2} \over {14}} = {{0.7} \over {14}} = {1 \over {20}}$$
According to thin lens formula
$${1 \over v} - {1 \over u} = {1 \over f}$$
Here, u = $$-$$40 cm
$$\therefore$$ $${1 \over v} - {1 \over { - 40}} = {1 \over {20}}$$ or $${1 \over v} = {1 \over {20}} - {1 \over {40}}$$ or v = 40 cm
Comments (0)


