JEE Advance - Physics (2012 - Paper 1 Offline - No. 6)

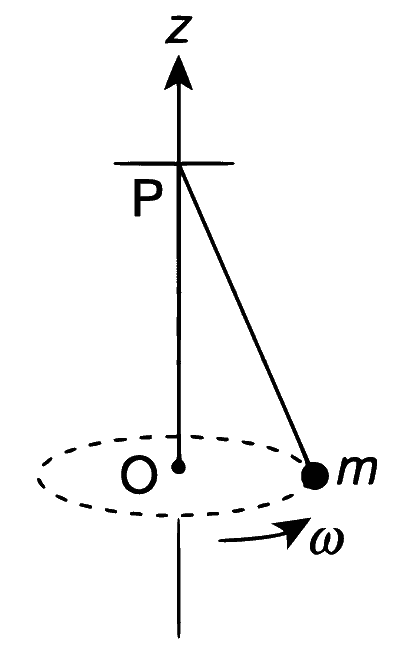
A small mass m is attached to a massless string whose other end is fixed at P as shown in the figure. The mass is undergoing circular motion in the xy-plane with centre at O and constant angular speed $$\omega$$. If the angular momentum of the system, calculated about O and P are denoted by $${\overrightarrow L _O}$$ and $${\overrightarrow L _P}$$, respectively, then

IIT-JEE 2012 Paper 1 Offline Physics - Rotational Motion Question 24 English

$${\overrightarrow L _O}$$ and $${\overrightarrow L _P}$$ do not vary with time.

$${\overrightarrow L _O}$$ varies with time while $${\overrightarrow L _P}$$ remains constant.

$${\overrightarrow L _O}$$ remains constant while $${\overrightarrow L _P}$$ varies with time.

$${\overrightarrow L _O}$$ and $${\overrightarrow L _P}$$ both vary with time.

Explanation

Angular momentum of a particle about a point is given by:

L = r $$\times$$ p = m (r $$\times$$ v)

For L_O

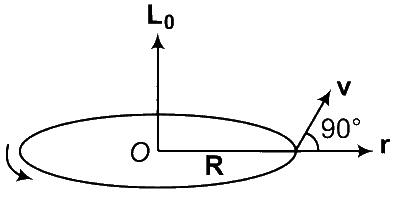
IIT-JEE 2012 Paper 1 Offline Physics - Rotational Motion Question 24 English Explanation 1

$$\left| L \right| = (mvr\sin \theta ) = m(R\omega )(R)\sin 90^\circ $$

$$ = m{R^2}\omega $$ = constant

Direction of L_O is always upwards. Therefore, complete L_O is constant, both in magnitude as well as direction.

For L_P

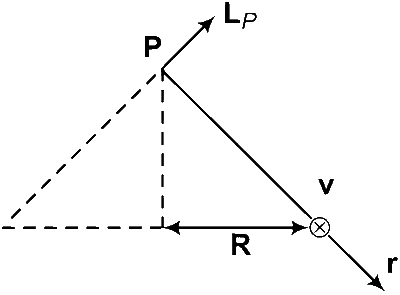
IIT-JEE 2012 Paper 1 Offline Physics - Rotational Motion Question 24 English Explanation 2

$$\left| {{L_P}} \right| = (mvr\sin \theta ) = m(R\omega )(l)\sin 90^\circ $$

$$ = (mRl\omega )$$

Magnitude of L_P will remain constant but direction of L_P keeps on changing.

JEE Advance - Physics (2012 - Paper 1 Offline - No. 6)

Explanation

Comments (0)