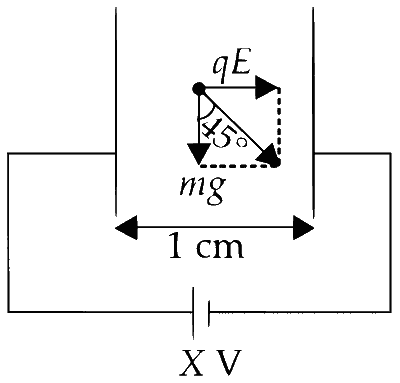
Given that the proton moves at a $45^{\circ}$ angle to the vertical, we can derive the electric field (E) as follows :

$ qE = mg $ or $ E = \frac{mg}{q} $

Since $ E = \frac{X}{d} $, we can substitute to find $ X $ :

$ \frac{X}{d} = \frac{mg}{q} $ or $ X = \frac{mgd}{q} $

Where :

• $ m = 1.67 \times 10^{-27} \, \mathrm{kg} $


• $ g = 10 \, \mathrm{m/s^2} $


• $ d = 1 \, \mathrm{cm} = 1 \times 10^{-2} \, \mathrm{m} $


• $ q = 1.6 \times 10^{-19} \, \mathrm{C} $

Substituting these values, we get :

$ \begin{aligned} X &= \frac{1.67 \times 10^{-27} \times 10 \times 1 \times 10^{-2}}{1.6 \times 10^{-19}} \, \mathrm{V} \\\\ &= \frac{1.67}{1.6} \times 10^{-9} \, \mathrm{V} \\\\ &= 1 \times 10^{-9} \, \mathrm{V} \end{aligned} $