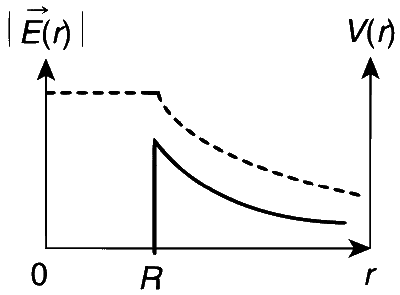
Consider a thin spherical shell of radius $ R $ with its center at the origin, carrying a uniform positive surface charge density. To understand how the electric field $ \left| \overrightarrow{E} \left( r \right) \right| $ and the electric potential $ V(r) $ vary with the distance $ r $ from the center, refer to the following details:

Electric Field due to a Uniformly Charged Thin Spherical Shell

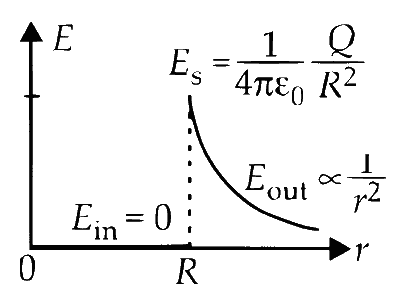
Inside the Shell

For $ r < R $, the electric field is given by:

$$ E_{\text{inside}} = 0 \quad [ r < R ] $$

On the Surface of the Shell

For $ r = R $, the electric field is:

$$ E_{\text{surface}} = \frac{1}{4 \pi \varepsilon_0} \frac{Q}{R^2} $$

Outside the Shell

For $ r > R $, the electric field is:

$$ E_{\text{outside}} = \frac{1}{4 \pi \varepsilon_0} \frac{Q}{r^2} \quad [ r > R ] $$

Below is a graphical representation of the electric field $ E $ variation with the distance $ r $ from the center:

Electric Potential due to a Uniformly Charged Thin Spherical Shell

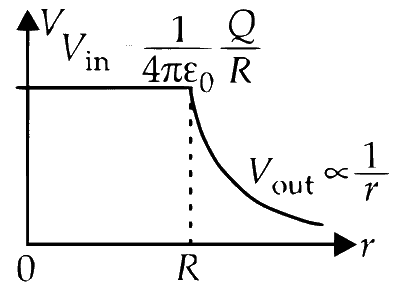
Inside the Shell

For $ r < R $, the electric potential is:

$$ V_{\text{inside}} = \frac{1}{4 \pi \varepsilon_0} \frac{Q}{R} $$

On the Surface of the Shell

For $ r = R $, the electric potential is:

$$ V_{\text{surface}} = \frac{1}{4 \pi \varepsilon_0} \frac{Q}{R} $$

Outside the Shell

For $ r > R $, the electric potential is:

$$ V_{\text{outside}} = \frac{1}{4 \pi \varepsilon_0} \frac{Q}{r} $$

Below is a graphical representation of the electric potential $ V $ variation with the distance $ r $ from the center: