JEE Advance - Physics (2012 - Paper 1 Offline - No. 19)
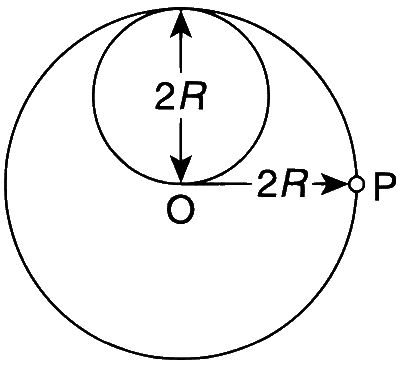
A lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure. The moment of inertia of this lamina about axes passing through O and P is IO and IP respectively. Both these axes are perpendicular to the plane of the lamina. The ratio IO/IP to the nearest integer is ____________.
Explanation
T = Total portion
R = Remaining portion and
C = Cavity and
Then, $${m_T} = \pi {(2R)^2}\sigma = 4\pi {R^2}\sigma $$
$${m_C} = \pi {(R)^2}\sigma = \pi {R^2}\sigma $$
For IP
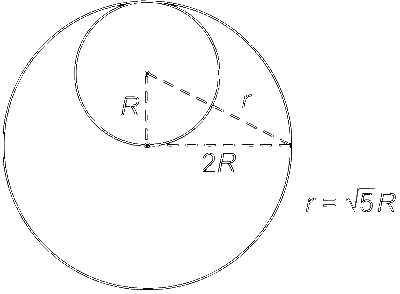
$${I_R} = {I_T} - {I_C}$$
$$ = {3 \over 2}{m_T}{(2R)^2} - \left[ {{1 \over 2}{m_C}{R^2} + {m_C}{r^2}} \right]$$
$$ = {3 \over 2}(4\pi {R^2}\sigma )(4{R^2}) - \left[ {{1 \over 2}(\pi {R^2}\sigma ) + (\pi {R^2}\sigma )(5{R^2})} \right]$$
$$ = (18.5\pi {R^4}\sigma )$$
For IO
$${I_R} = {I_T} - {I_C}$$
$$ = {1 \over 2}{m_T}{(2R)^2} - {3 \over 2}{m_C}{R^2}$$
$$ = {1 \over 2}(4\pi {R^2}\sigma )(4{R^2}) - {3 \over 2}(\pi {R^2}\sigma )({R^2})$$
$$ = 6.5\pi {R^4}\sigma $$
$$\therefore$$ $${{{I_P}} \over {{I_O}}} = {{18.5\pi {R^4}\sigma } \over {6.5\pi {R^4}\sigma }} = 2.846$$
Therefore, the nearest integer is 3.
Comments (0)


