JEE Advance - Physics (2012 - Paper 1 Offline - No. 17)
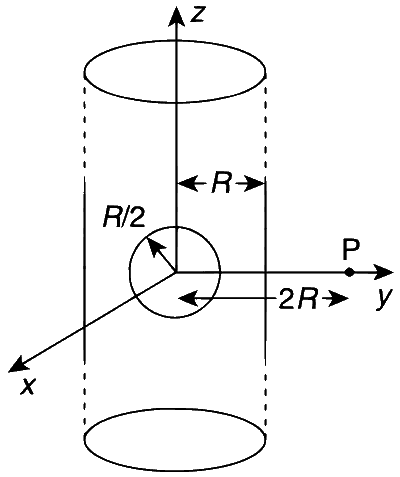
An infinitely long solid cylinder of radius R has a uniform volume charge density $$\rho$$. It has a spherical cavity of radius R/2 with its centre on the axis of the cylinder, as shown in the figure. The magnitude of the electric field at the point P, which is at a distance 2R from the axis of the cylinder, is given by the expression $${{23\rho R} \over {16k{\varepsilon _0}}}$$. The value of k is _____________.
Explanation
Electric field at point P due to long uniformly charged solid cylinder is
$${E_1} = {{\rho {R^2}} \over {2{\varepsilon _0}(2R)}} = {{\rho R} \over {4{\varepsilon _0}}}$$
Electric field at point P due to spherical cavity is
$${E_1} = {1 \over {4\pi {\varepsilon _0}}}{{\rho {4 \over 3}\pi {{\left( {{R \over 2}} \right)}^3}} \over {{{(2R)}^2}}} = {{\rho R} \over {96{\varepsilon _0}}}$$
The electric field at the point P is
$$ = {E_1} - {E_2}$$
$$ = {{\rho R} \over {4{\varepsilon _0}}} - {{\rho R} \over {96{\varepsilon _0}}} = {{\rho R} \over {4{\varepsilon _0}}}\left[ {1 - {1 \over {24}}} \right] = {{23\rho R} \over {96{\varepsilon _0}}} = {{23\rho R} \over {(16)6{\varepsilon _0}}} = {{23\rho R} \over {16k{\varepsilon _0}}}$$
$$\therefore$$ $$k = 6$$
Comments (0)


