JEE Advance - Physics (2012 - Paper 1 Offline - No. 16)
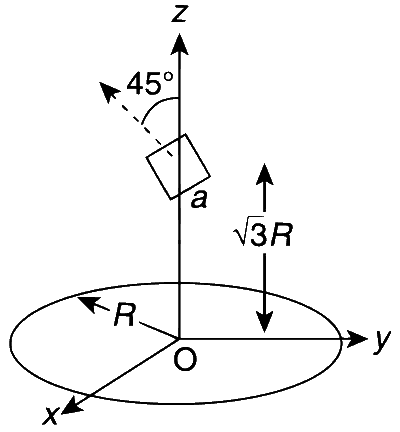
A circular wire loop of radius R is placed in the xy plane centred at the origin O. A square loop of side a(a << R) having two turns is placed with its centre at z = $$\sqrt3$$R along the axis of the circular wire loop, as shown in the figure. The plane of the square loop makes an angle of 45$$^\circ$$ with respect to z-axis. If the mutual inductance between the loops is given by $${{{\mu _0}{a^2}} \over {{2^{p/2}}R}}$$, then the value of p is ___________.
Explanation
The magnetic flux through a wire loop with $ n $ turns, an area vector $ \vec{S} $, placed in a uniform magnetic field $ \vec{B} $, is given by the equation $ \phi = n \vec{B} \cdot \vec{S} $. For a circular loop of radius $ r $ that carries a current $ i $, the magnetic field at an axial point located a distance $ z $ from the center of the loop can be expressed as :
$|\vec{B}|=\frac{\mu_0 i r^2}{2\left(r^2+z^2\right)^{3 / 2}}$
By substituting $ r = R $ and $ z = \sqrt{3} R $ into the expression for the magnetic field at an axial point of a circular loop, we get the magnetic field $ |\vec{B}| $ as follows:
The formula for the magnetic field at an axial point $ z $ from a circular loop of radius $ r $ carrying a current $ i $ is given by:
$ B = \frac{\mu_0 i r^2}{2 (r^2 + z^2)^{3/2}} $
Substituting $ r = R $ and $ z = \sqrt{3} R $ into this formula, we get:
$ B = \frac{\mu_0 i R^2}{2 (R^2 + (\sqrt{3} R)^2)^{3/2}} $
Simplify the expression inside the parentheses:
$ B = \frac{\mu_0 i R^2}{2 (R^2 + 3R^2)^{3/2}} $
$ B = \frac{\mu_0 i R^2}{2 (4R^2)^{3/2}} $
$ B = \frac{\mu_0 i R^2}{2 (4^{3/2} R^3)} $
$ 4^{3/2} = 8 $
$ B = \frac{\mu_0 i R^2}{2 (8 R^3)} $
$ B = \frac{\mu_0 i R^2}{16 R^3} $
$ B = \frac{\mu_0 i}{16 R} $
Thus, the magnetic field at the axial point $ z = \sqrt{3} R $ is:
$ |\vec{B}| = \frac{\mu_0 i}{16 R} $
This magnetic field is directed along the $ z $-axis and can be considered uniform at the location of the square loop (since $ a \ll R $). Consequently, $ \vec{B} $ forms an angle of $ 45^\circ $ with the area vector $ \vec{S} $ (where $ |\vec{S}| = a^2 $) of the square loop. The magnetic flux through the square loop and the mutual inductance of the loops are given by:
$\begin{aligned} & \phi=n|\vec{B}||\vec{S}| \cos 45^{\circ}=2 \cdot \frac{\mu_0 i}{16 R} \cdot a^2 \cdot \frac{1}{\sqrt{2}}=\frac{\mu_0 i a^2}{2^{7 / 2} R}, \\\\ & M=\frac{\phi}{i}=\frac{\mu_0 a^2}{2^{7 / 2} R} .\end{aligned}$
Comments (0)


