JEE Advance - Physics (2012 - Paper 1 Offline - No. 10)
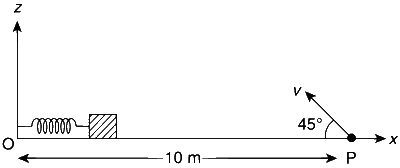
A small block is connected to one end of a massless spring of un-stretched length 4.9 m. The other end of the spring (see the figure) is fixed. The system lies on a horizontal frictionless surface. The block is stretched by 0.2 m and released from rest at t = 0. It then executes simple harmonic motion with angular frequency $$\omega$$ = ($$\pi$$/3) rad/s. Simultaneously, at t = 0, a small pebble is projected with speed v from point P at an angle of 45$$^\circ$$ as shown in the figure. Point O is at a horizontal distance of 10 m from O. If the pebble hits the block at t = 1 s, the value of v is (take g = 10 m/s2)
Explanation
Since, the block starts executing simple harmonic motion from extreme position, we have
$$x = a\cos \omega t$$
At 1 s, we have
$$x = 0.2\cos \left( {{\pi \over 3}} \right) = 0.1\,m$$
That is, the block is at a distance 5.1 $$-$$ 0.10 = 5 m from O, which is the range of the bebble as well. Now,
$$R = {{{v^2}\sin 2\alpha } \over g}$$
$$S = {{{v^2}\sin 2(\pi /4)} \over {10}}$$
Therefore, $$v = \sqrt {50} $$ m/s
Alternate Method :
Since, pebble strikes the oscillating mass after 1 sec., its time of flight is $1 \mathrm{~s}$
$$ \begin{aligned} & 1=\frac{2 v \sin 45^{\circ}}{\mathrm{g}}=\frac{\sqrt{2} v}{10} \\\\ & v=\frac{10}{\sqrt{2}}=5 \sqrt{2}=\sqrt{50} \mathrm{~m} / \mathrm{s} \end{aligned} $$
Comments (0)


