Sign In

JEE Advance - Physics (2012 - Paper 1 Offline - No. 1)

A cubical region of side $$a$$ has its center at the origin. It encloses three fixed point charges, $$-q$$ at $$\left( {0, - a/4,0} \right), + 3q$$ at $$\left( {0,0,0} \right)$$ and $$-q$$ at $$\left( {0, + a/4,0} \right).$$ Choose the correct option(s)
IIT-JEE 2012 Paper 1 Offline Physics - Electrostatics Question 47 English
The net electric flux crossing the plane $$x=+a/2$$ is equal to the net electric flux crossing the plane $$x=-a/2$$
The net electric flux crossing the plane $$y=+a/2$$ is more than the net electric flux crossing the plane $$y=-a/2.$$
The net electric flux crossing the entire region is $${q \over {{\varepsilon _0}}}$$
The net electric flux crossing the plane $$z = + a/2$$ is equal to the net electric flux crossing the plane $$x=+a/2.$$

Explanation

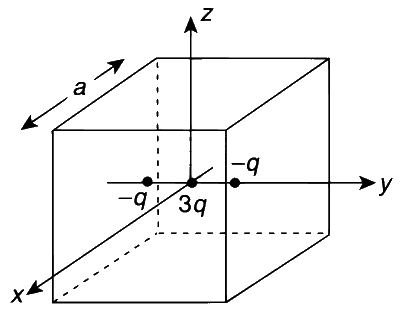
The positions of all charges are symmetric about the planes $$x = +\frac{a}{2}$$ and $$x = -\frac{a}{2}$$. Therefore, the net electric flux crossing the plane $$x = +\frac{a}{2}$$ is equal to the net electric flux crossing the plane $$x = -\frac{a}{2}$$.

Similarly, the net electric flux crossing the plane $$y = +\frac{a}{2}$$ is equal to the net electric flux crossing the plane $$y = -\frac{a}{2}$$.

According to Gauss's law, the net electric flux crossing the entire region is given by:

$$ \phi = \frac{q_{\text{inside}}}{\varepsilon_0} = \frac{3q - q - q}{\varepsilon_0} = \frac{q}{\varepsilon_0} $$

The charges are symmetrically placed about the planes $$z = +\frac{a}{2}$$ and $$x = +\frac{a}{2}$$. Thus, the net electric flux crossing the plane $$z = +\frac{a}{2}$$ is equal to the net electric flux crossing the plane $$x = +\frac{a}{2}$$.

Comments (0)

Advertisement