JEE Advance - Physics (2011 - Paper 2 Offline - No. 6)
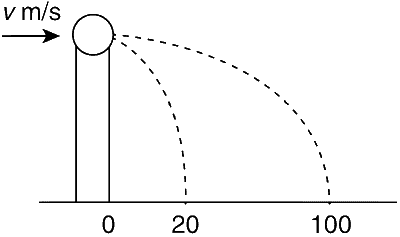
A ball of mass 0.2 kg rests on a vertical post of height 5 m. A bullet of mass 0.01 kg, traveling with a velocity V m/s in a horizontal direction, hits the center of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of 20 m and the bullet at a distance of 100 m from the foot of the post. The velocity V of the bullet is
Explanation
The time of flight for the bullet is same as that of the ball and is given by
$$t = \sqrt {{{2h} \over g}} = \sqrt {{{2 \times 5} \over {10}}} = 1\,s$$
Just after the collision, the velocity of bullet (v1) is related to its range (R1) by v1t = R1 which gives v1 = 100 m/s. Similarly, the velocity of the ball is v2 = 20 m/s. Consider the bullet and the ball together as a system. Along the direction of collision, there is no external force on the system. Hence, linear momentum of the system in the direction of collision is conserved. The linear momentum of the system before and after the collision are
$${p_i} = {m_1}V$$,
$${p_f} = {m_1}{v_1} + {m_2}{v_2}$$.
The conservation of linear momentum, $${p_i} = {p_f}$$, gives
$$V = {{{m_1}{v_1} + {m_2}{v_2}} \over {{m_1}}}$$
$$ = {{(0.01)(100) + (0.2)(20)} \over {0.01}} = 500$$ m/s.
Comments (0)


