Sign In

JEE Advance - Physics (2011 - Paper 2 Offline - No. 4)

A point mass is subjected to two simultaneous sinusoidal displacements in x-direction, $${x_1}\left( t \right) = A\sin \omega t$$ and $${x_2}\left( t \right) = A\sin \left( {\omega t + {{2\pi } \over 3}} \right)$$. Adding a third sinusoidal displacement $${x_3}\left( t \right) = B\sin \left( {\omega t + \phi } \right)$$ brings the mass to a complete rest. The values of B and $$\phi $$ are
$$\sqrt 2 A,{{3\pi } \over 4}$$
$$A,{{4\pi } \over 3}$$
$$\sqrt 3 A,{{5\pi } \over 6}$$
$$A,{\pi \over 3}$$

Explanation

Here, $${x_1} = A\sin \omega t$$

$${x_2} = A\sin \left( {\omega t + {{2\pi } \over 3}} \right)$$

$$\therefore$$ $${x_1} + {x_2} = A\sin \omega t + A\sin \left( {\omega t + {{2\pi } \over 3}} \right)$$

$$ = A\sin \omega t + A\left[ {\sin \omega t\cos {{2\pi } \over 3} + \cos \omega t\sin {{2\pi } \over 3}} \right]$$

$$ = A\sin \omega t + A\left[ {\sin \omega t\left( { - {1 \over 2}} \right) + \cos \omega t\left( {{{\sqrt 3 } \over 2}} \right)} \right]$$

$$ = {A \over 2}\sin \omega t + {{\sqrt 3 } \over 2}A\cos \omega t = A\left[ {\sin \omega t\cos {\pi \over 3} + \cos \omega t\sin {\pi \over 3}} \right]$$

$$ = A\sin \left( {\omega t + {\pi \over 3}} \right)$$

$$\because$$ $${x_1} + {x_2} + {x_3} = 0$$

$$ \Rightarrow {x_3} = - ({x_1} + {x_2}) = - A\sin \left( {\omega t + {\pi \over 3}} \right)$$

$$ = A\sin \left( {\omega t + \pi + {\pi \over 3}} \right)$$

$${x_3} = A\sin \left( {\omega t + {{4\pi } \over 3}} \right)$$

$$\because$$ $${x_3} = B\sin (\omega t + \phi )$$

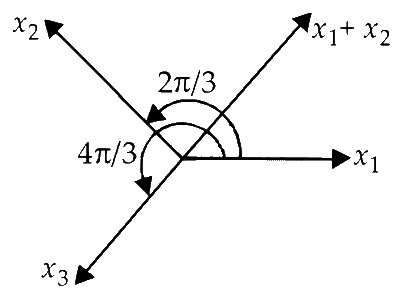
IIT-JEE 2011 Paper 2 Offline Physics - Simple Harmonic Motion Question 20 English Explanation

Hence, $$B = A,\,\phi = {{4\pi } \over 3}$$

Comments (0)

Advertisement