JEE Advance - Physics (2011 - Paper 2 Offline - No. 20)

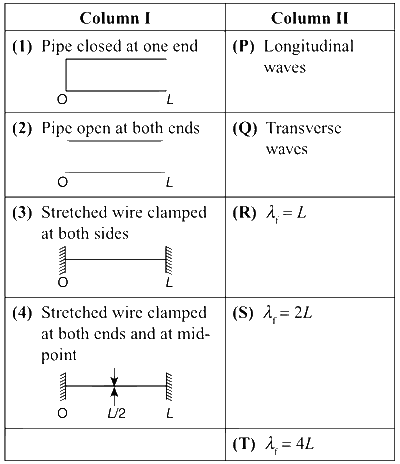
Column I shows four systems, each of the same length L, for producing standing waves. The lowest possible natural frequency of a system is called its fundamental frequency, whose wavelength is denoted as $$\lambda$$_f. Match each system with statements given in Column II describing the nature and wavelength of the standing waves :

IIT-JEE 2011 Paper 2 Offline Physics - Waves Question 17 English

(A)$$\to$$(T); (B)$$\to$$(P), (S); (C)$$\to$$(Q), (S); (D)$$\to$$(Q)

(A)$$\to$$(P), (T); (B)$$\to$$(P); (C)$$\to$$(Q), (S); (D)$$\to$$(Q)

(A)$$\to$$(P); (B)$$\to$$(P), (S); (C)$$\to$$(Q); (D)$$\to$$(Q), (R)

(A)$$\to$$(P), (T); (B)$$\to$$(P), (S); (C)$$\to$$(Q), (S); (D)$$\to$$(Q), (R)

Explanation

(1) For a pipe closed at one end, we have

$${{{\lambda _f}} \over 4} = L$$ or $${\lambda _f} = 4L$$

Therefore, the sound waves are longitudinal.

(2) For a pipe open at both ends, we have

$${{{\lambda _f}} \over 2} = L$$ or $${\lambda _f} = 2L$$

Therefore, the sound waves are longitudinal.

(3) For a stretched wire clamped at both ends, we have

$${{{\lambda _f}} \over 2} = L$$

Vibration on the string is transverse.

(4) For a stretched wire clamped at both ends and at mid-point, we have

$${{{\lambda _f}} \over 2} = {L \over 2} \Rightarrow {\lambda _f} = L$$

Therefore, the vibration on the string is transverse.

JEE Advance - Physics (2011 - Paper 2 Offline - No. 20)

Explanation

Comments (0)