JEE Advance - Physics (2011 - Paper 2 Offline - No. 19)
One mole of a monatomic gas is taken through a cycle ABCDA as shown in the PV diagram. Column II give the characteristics involved in the cycle. Match them with each of the processes given in Column I.
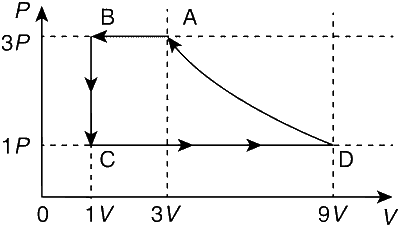
| Column I | Column II | ||
|---|---|---|---|
| (A) | Process A$$ \to $$ B | (P) | Internal energy decreases. |
| (B) | Process B$$ \to $$C | (Q) | Internal energy increase. |
| (C) | Process C$$ \to $$D | (R) | Heat is lost. |
| (D) | Process D$$ \to $$A | (S) | Heat is gained. |
| (T) | Work is done on the gas. |
Explanation
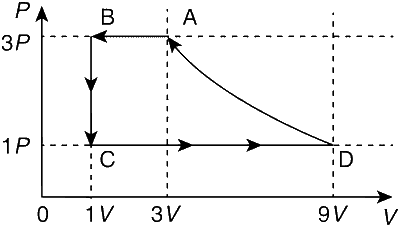
Process A $$\to$$ B,
It is a isobaric process
P = constant, V $$\propto$$ T
$$\because$$ VB < VA $$\Rightarrow$$ TB < TA
$$\Delta$$U = nCV$$\Delta$$T = $$-$$ve
Hence internal energy decreases.
$$\Delta$$Q = nCP$$\Delta$$T = $$-$$ve
Hence heat is lost.
$$\Delta$$W = nR$$\Delta$$T = $$-$$ve
Hence, work is done on the gas.
Process, B $$\to$$ C,
It is a isochoric process.
V = constant, P $$\propto$$ T
$$\because$$ PC < PB $$\Rightarrow$$ TC < TB
$$\Delta$$U = nCV$$\Delta$$T = $$-$$ve
Hence, internal energy decreases.
$$\Delta$$W = 0, $$\Delta$$Q = $$\Delta$$U = $$-$$ve
Hence, heat is lost.
Process C $$\to$$ D,
It is a isobaric process.
P = constant, V $$\propto$$ T
$$\because$$ VD > VC $$\Rightarrow$$ TD > TC
$$\Delta$$U = nCV$$\Delta$$T = +ve
Hence internal energy increases.
$$\Delta$$Q = nCP$$\Delta$$T = +ve
Hence, heat is gained.
$$\Delta$$W = nR$$\Delta$$T = +ve
Hence, work is done by the gas.
Process, D $$\to$$ A
According to ideal gas equation
$${{{P_A}{V_A}} \over {{T_A}}} = {{{P_D}{V_D}} \over {{T_D}}} \Rightarrow {{(3P)(3V)} \over {{T_A}}} = {{(P)(9V)} \over {{T_D}}} \Rightarrow {T_D} = {T_A}$$
Hence, it is a isothermal process.
$$\therefore$$ $$\Delta$$U = 0
$$\because$$ VA < VD
$$\Delta$$W = $$-$$ve, hence work done is done on the gas.
$$\Delta$$Q = $$\Delta$$W = $$-$$ve, hence heat is lost.
Comments (0)


