JEE Advance - Physics (2011 - Paper 2 Offline - No. 18)
Water (with refractive index = 4/3) in a tank is 18 cm deep. Oil of refractive index 7/4 lies on water making a convex surface of radius of curvature R = 6 cm as shown. Consider oil to act a thin lens. An object S is placed 24 cm above water surface. The location of its image is at x cm above the bottom of the tank. Then x is __________.
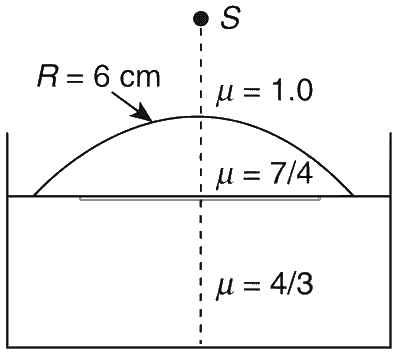
Explanation
We have
$${{{n_2}} \over v} - {{{n_1}} \over u} = {{{n_1} - {n_2}} \over R}$$
For the first refracting surface (air-oil), we have n2 = 7/4; n1 = 1; R = 6 cm. Therefore,
$${7 \over {4{v_1}}} - {1 \over {24}} = {{ - (7/4)} \over 6}$$
or v1 = 21 cm and for the second interface (water-oil), we have
$${n_1} = {7 \over 4};{n_2} = {4 \over 3}u = {v_1};R = \infty $$
Therefore,
$${4 \over {3{v_2}}} - {7 \over {4 \times 21}} = 0$$
v2 = 16 cm and v2 + x = height of water.
Therefore,
$$x = 18 - 16 = 2$$
Comments (0)


