JEE Advance - Physics (2011 - Paper 2 Offline - No. 12)
Two solid spheres A and B of equal volumes but of different densities dA and dB are connected by a string. They are fully immersed in a fluid of density dF. They get arranged into an equilibrium state as shown in the figure with a tension in the string. The arrangement is possible only if
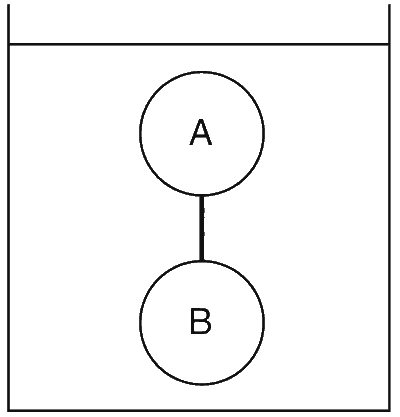
Explanation
Let V be the volume of each sphere and let T be the tension in the string.
Buoyant force on sphere A is UA = dFVg
Buoyant force on sphere B is UB = dFVg
Weight of A is WA = dAVg
Weight of B is WB = dBVg
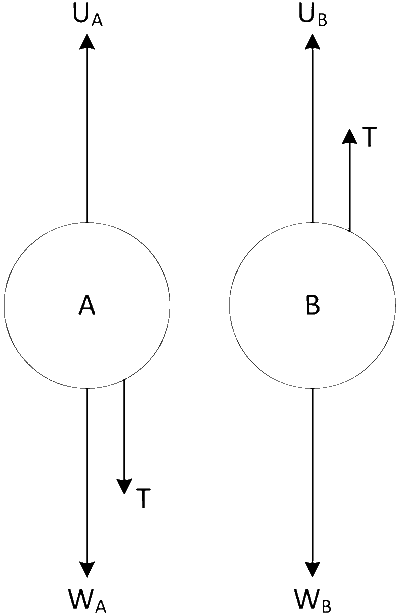
The free body diagrams of A and B are as follows. (see Fig. 11.34)
For equilibrium,
UA = T + WA and UB + T = WB
i.e. dFVg = T + dAVg ..... (i)
and dFVg + T = dBVg .... (ii)
From Eq. (i) $${d_F} = {T \over {Vg}} + {d_A}$$. Hence, dF > dA. So choice (a) is correct.
From Eq. (ii) $${d_B} = {T \over {Vg}} + {d_F}$$. Hence dB > dF. So choice (b) is also correct.
Eliminating T from Eqs. (i) and (ii) we get $$2{d_F} = {d_A} + {d_B}$$, which is choice (d).
So, the correct choices are (a), (b) and (d).
Comments (0)


