JEE Advance - Physics (2011 - Paper 2 Offline - No. 11)
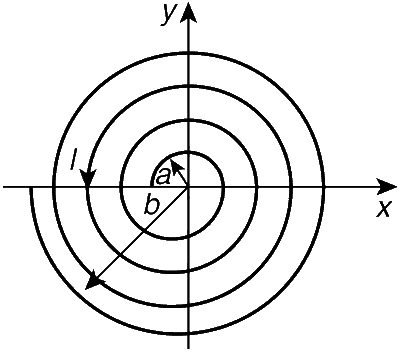
A long insulated copper wire is closely wound as a spiral of N turns. The spiral has inner radius a and outer radius b. The spiral lies in the xy-plane and a steady current I flows through the wire. The z-component of the magnetic field at the centre of the spiral is
Explanation
Magnetic field at the centre of a circular loop of radius r and carrying a current $$I = {{{\mu _0}I} \over {2r}}$$. The direction of the field is along z-direction if the current is anticlockwise.
Consider a small element of width dr. The current through the element is
$$dI = {{total\,current\,in\,spiral} \over {total\,width\,of\,spiral}} \times width\,of\,element$$
$$ = {{Idr} \over {(b - a)}}$$
$$\therefore$$ $$B = \int\limits_a^b {{{{\mu _0}NdI} \over {2r}} = \int\limits_a^b {{{{\mu _0}NI} \over {2(b - a)}}{{dr} \over r}} } $$
$$ = {{{\mu _0}NI} \over {2(b - a)}}\int\limits_a^b {{{dr} \over r} = {{{\mu _0}NI} \over {2(b - a)}}\ln \left( {{b \over a}} \right)} $$
Comments (0)


