JEE Advance - Physics (2011 - Paper 1 Offline - No. 9)
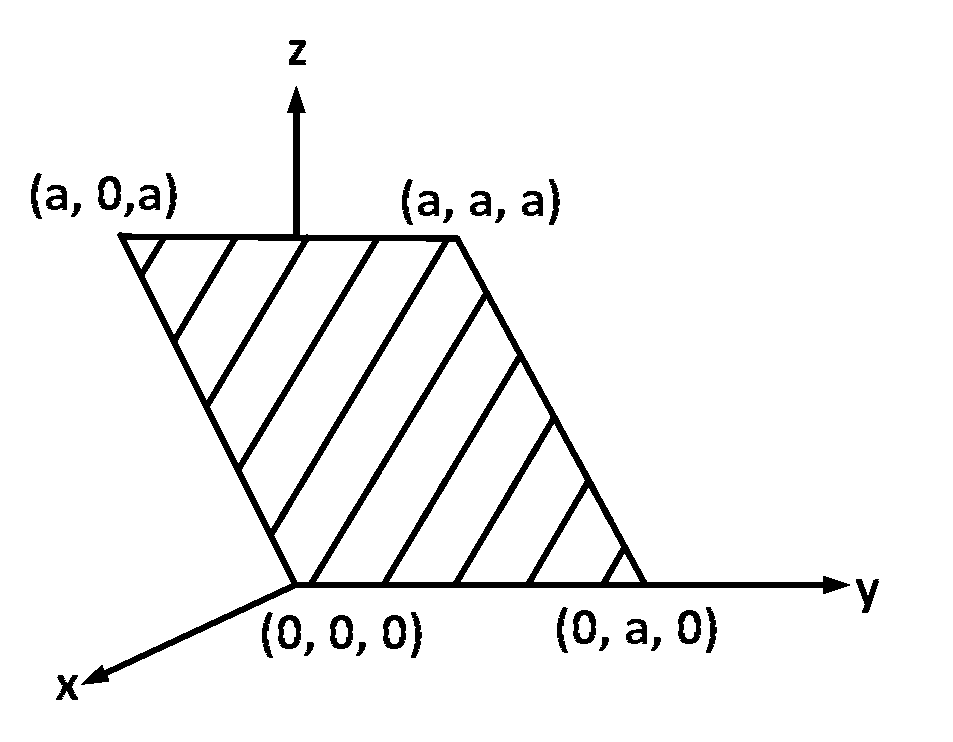
Consider an electric field $$\overrightarrow E = {E_0}\widehat x$$ where $${E_0}$$ is a constant. The flux through the shaded area (as shown in the figure) due to this field is

$$2{E_0}{a_2}$$
$$\sqrt 2 {E_0}{a^2}$$
$${E_0}\,{a^2}$$
$${{{E_0}{a^2}} \over {\sqrt 2 }}$$
Explanation
The flux through an area $$\overrightarrow S $$ due to an electric field $$\overrightarrow E $$ is given by
$$\phi = \oint {\overrightarrow E \,.\,d\overrightarrow S } $$
$$ = \overrightarrow E \,.\,\oint {d\overrightarrow S = \overrightarrow E \,.\,\overrightarrow S } $$ ($$\because$$ $$\overrightarrow E $$ is a constant.) ...... (1)
The area of the shaded region is the cross product of vectors representing the two sides i.e.,
$$\overrightarrow S = (a\widehat j) \times (a\widehat i + a\widehat k) = {a^2}(\widehat i - \widehat k)$$ ...... (2)
Use equations (1) and (2) to get
$$\phi = ({E_0}\widehat i)\,.\,{a^2}(\widehat i - \widehat k) = {E_0}{a^2}$$.
Comments (0)


