The moment of inertia of each sphere about an axis passing through its centre is $${2 \over 5}m{r^2}$$.

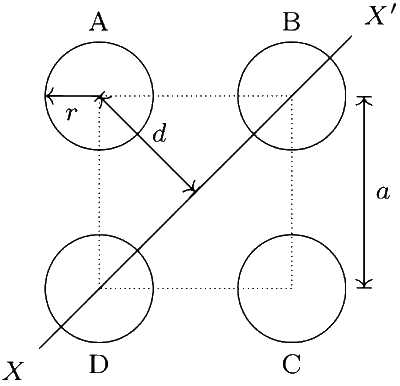
The moment of inertia of sphere B and sphere D about X $$-$$ X' is

$${I_B} = {I_D} = {2 \over 5}m{r^2}$$.

Using parallel axes theorem, the moment of inertia of sphere A and sphere C about X $$-$$ X' is

$${I_A} = {I_C} = {2 \over 5}m{r^2} + m{d^2}$$

The moment of inertia of the system about the diagonal is

$$I = {I_A} + {I_B} + {I_C} + {I_D} = {8 \over 5}m{r^2} + 2m{d^2}$$

$$m = 0.5$$ kg

$$d = {a \over {\sqrt 2 }} = {4 \over {\sqrt 2 }}$$ cm

$$r = {{\sqrt 5 } \over 2}$$ cm

$$\therefore$$ $$I = {8 \over 5} \times 0.5 \times {\left( {{{\sqrt 5 } \over 2} \times {{10}^{ - 2}}} \right)^2} + 2 \times 0.5 \times {\left( {{4 \over {\sqrt 2 }} \times {{10}^{ - 2}}} \right)^2}$$

$$ = 9 \times {10^{ - 4}}$$ kg m²

Hence, $$N = 9$$