JEE Advance - Physics (2011 - Paper 1 Offline - No. 4)
A block is moving on an inclined plane making an angle $$45^\circ $$ with the horizontal and the coefficient of friction is $$\mu $$. The force required to just push it up the inclined plane is 3 times the force required to just
prevent it from sliding down. If we define N = 10 $$\mu $$, then N is
Answer
5
Explanation
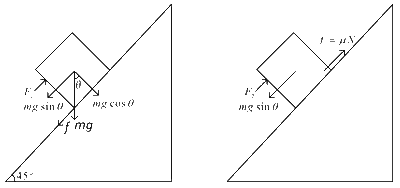
The pushing force $${F_1} = mg\sin \theta + f$$
$$\therefore$$ $${F_1} = mg\sin \theta + \mu mg\cos \theta = mg(\sin \theta + \mu \cos \theta )$$
The force required to just prevent it from sliding down
$${F_2} = mg\sin \theta - \mu N = mg(\sin \theta - \mu \cos \theta )$$
Given, $${F_1} = 3{F_2}$$
$$\therefore$$ $$\sin \theta + \mu \cos \theta = 3(\sin \theta - \mu \cos \theta )$$
$$\therefore$$ $$1 + \mu = 3(1 - \mu )$$ [$$\because$$ $$\sin \theta = \mu \cos \theta $$]
$$\therefore$$ $$4\mu = 2$$
$$\therefore$$ $$\mu = 0.5$$
$$\therefore$$ $$N = 10\mu = 5$$
Comments (0)


