JEE Advance - Physics (2011 - Paper 1 Offline - No. 23)
A long circular tube of length 10 m and radius 0.3 m carries a current I along its curved surface as shown. A wire-loop of resistance 0.005 $$\Omega$$ and of radius 0.1 m is placed inside the tube with its axis coinciding with the axis of the tube. The current varies as $$I = {I_0}\cos (300t)$$, where I0 is constant. If the magnetic moment of the loop is $$N{\mu _0}{I_0}\sin (300t)$$, then N is ___________.
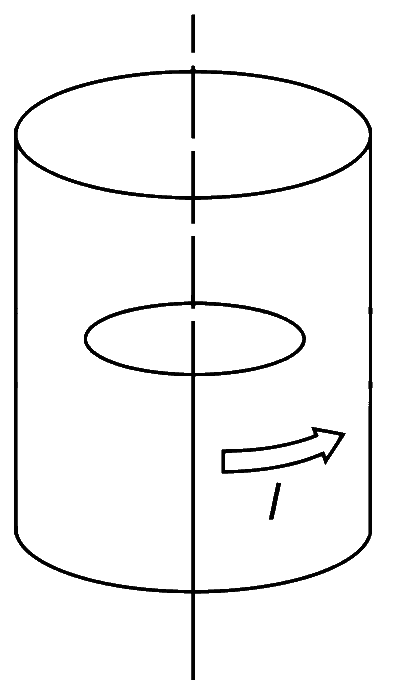
Explanation
The flux through the ring is
$$\phi = B\pi {r^2}$$
Assuming the cylinder as a solenoid with close winding, we have
$$B = {{{\mu _0}I} \over L}$$
Therefore,
$$\phi = \left( {{{{\mu _0}I} \over L}} \right)\pi {r^2}\cos 300t$$
The induced emf is
$$\varepsilon = {{ - d\phi } \over {dt}} = 300\left( {{{{\mu _0}I} \over L}} \right)\pi {r^2}\sin 300t$$
Therefore, the current induced is
$$i = {\varepsilon \over R} = \left( {{{\pi {r^2}300} \over {RL}}} \right){\mu _0}{I_0}\sin 300t$$
The magnetic moment is
M = Current $$\times$$ Area of loop
Therefore,
$$m = \left( {{{{{(3.14)}^2} \times {{(0.1)}^4} \times 300} \over {0.005 \times 10}}} \right){\mu _0}{I_0}\sin 300t$$
$$ = 6{\mu _0}{I_0}\sin 300t$$
Hence, N = 6.
Comments (0)


