JEE Advance - Physics (2011 - Paper 1 Offline - No. 21)
Four point charges, each of +q, are rigidly fixed at the four corners of a square planar soap film of side a. The surface tension of the soap film is $$\gamma$$. The system of charges and planar film are in equilibrium, and $$a = k{\left[ {{{{q^2}} \over \gamma }} \right]^{1/N}}$$, where k is a constant. Then N is __________.
Answer
3
Explanation
The net force on one of the charges due to other charges is
$$F = {{2k{q^2}} \over {{a^2}}} + {{k{q^2}} \over {2{a^2}}} = {5 \over 2}\left( {{{k{q^2}} \over {{a^2}}}} \right)$$
where $$k = {1 \over {4\pi \varepsilon }}$$. Here, as shown in the figure, line AB divided the soap film into two equal parts. The free-body diagram of half part is also depicted in the figure here.
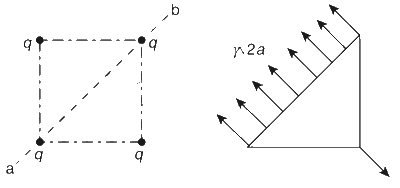
At equilibrium, the surface tension balances the force.
Therefore,
$${F_{surface}} = 2\sqrt 2 a\gamma $$
That is, $$2\sqrt 2 a\gamma = {5 \over 2}\left( {{{k{q^2}} \over {{a^2}}}} \right)$$
$$ \Rightarrow {a^3} = {5 \over {4\sqrt 2 }}\left( {{{{q^2}} \over \gamma }} \right)$$
Therefore,
a = Any constant $$ \times {\left( {{{{q^2}} \over \gamma }} \right)^{1/3}}$$
Hence, N = 3.
Comments (0)


