Sign In

JEE Advance - Physics (2011 - Paper 1 Offline - No. 18)

Phase space diagrams are useful tools in analyzing all kinds of dynamical problems. They are especially useful in studying the changes in motion as initial position and momentum are changed. Here we consider some simple dynamical systems in one-dimension. For such systems, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown int he figure. We use the sign convention in which position or momentum upwards (or to right) is positive and downwards (or to left) is negative.

Phase space diagrams are useful tools in analyzing all kinds of dynamical problems. They are especially useful in studying the changes in motion as initial position and momentum are changed. Here we consider some simple dynamical systems in one-dimension. For such systems, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown int he figure. We use the sign convention in which position or momentum upwards (or to right) is positive and downwards (or to left) is negative.

Phase space diagrams are useful tools in analyzing all kinds of dynamical problems. They are especially useful in studying the changes in motion as initial position and momentum are changed. Here we consider some simple dynamical systems in one-dimension. For such systems, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown int he figure. We use the sign convention in which position or momentum upwards (or to right) is positive and downwards (or to left) is negative.

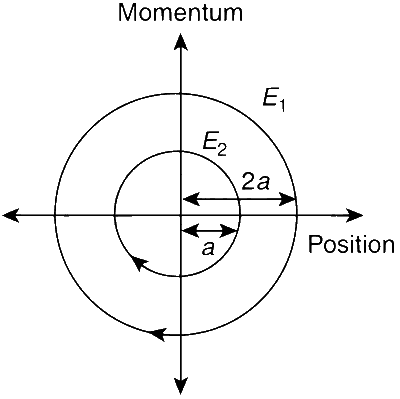
The phase space diagram for simple harmonic motion is a circle centred at the origin. In the figure, the two circles represent the same oscillator but for different initial conditions, and E1 and E2 are the total mechanical energies respectively. Then

IIT-JEE 2011 Paper 1 Offline Physics - Simple Harmonic Motion Question 13 English

E1 = $$\sqrt2$$E2
E1 = 2E2
E1 = 4E2
E1 = 16E2

Explanation

Energy of simple harmonic oscillator is

$$E = {1 \over 2}k{A^2}$$

where k is the force constant and A the amplitude of the oscillator. Since the oscillator is the same, the value of k is the same. Hence

$${E_1} = {1 \over 2}kA_1^2$$ and $${E_2} = {1 \over 2}kA_2^2$$

$$\therefore$$ $${{{E_1}} \over {{E_2}}} = {\left( {{{{A_1}} \over {{A_2}}}} \right)^2}$$

Now, A1 = maximum value of displacement of oscillator having energy E1 = 2a and A2 = a. Therefore

$${{{E_1}} \over {{E_2}}} = {\left( {{{2a} \over a}} \right)^2} = 4$$. So, $${E_1} = 4{E_2}$$

Comments (0)

Advertisement