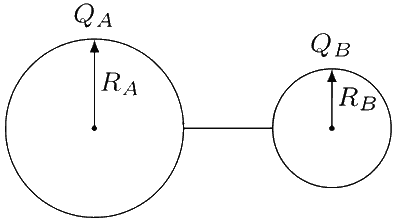
When connected by a wire, charges on A and B are redistributed until potential on both becomes equal. After the charge redistribution, A and B are not influenced by each other because they are far apart. Thus, $$E_A^{inside} = 0$$ as field inside a conducting shell is zero.

So choice (a) is correct.

Let Q_A and Q_B are the charges on metal shell A and metal sphere B after they are connected by a wire. Since their electric potentials will be equal,

V_A = V_B

$$ \Rightarrow {{{Q_A}} \over {4\pi {\varepsilon _0}{R_A}}} = {{{Q_B}} \over {4\pi {\varepsilon _0}{R_B}}} \Rightarrow {{{Q_A}} \over {{Q_B}}} = {{{R_A}} \over {{R_B}}}$$

Since $${R_B} < {R_A}$$, $${Q_A} > {Q_B}$$. So choice (b) is correct.

Now, $${\sigma _A} = {{{Q_A}} \over {4\pi R_A^2}}$$ and $${\sigma _B} = {{{Q_B}} \over {4\pi R_B^2}}$$

$$\therefore$$ $${{{\sigma _A}} \over {{\sigma _B}}} = {{{Q_A}} \over {{Q_B}}} \times {\left( {{{{R_B}} \over {{R_A}}}} \right)^2} = {{{R_A}} \over {{R_B}}} \times {\left( {{{{R_B}} \over {{R_A}}}} \right)^2} = {{{R_B}} \over {{R_A}}}$$

Hence, choice (c) is also correct.

Electric fields on the surface of shell and sphere are

$${E_A} = {{{\sigma _A}} \over {{\varepsilon _0}}}$$

and $${E_B} = {{{\sigma _B}} \over {{\varepsilon _0}}}$$

$$\therefore$$ $${{{E_A}} \over {{E_B}}} = {{{\sigma _A}} \over {{\sigma _B}}} < 1$$, i.e. $${E_A} < {E_B}$$

So, choice (d) is also correct. All the four choices are correct.