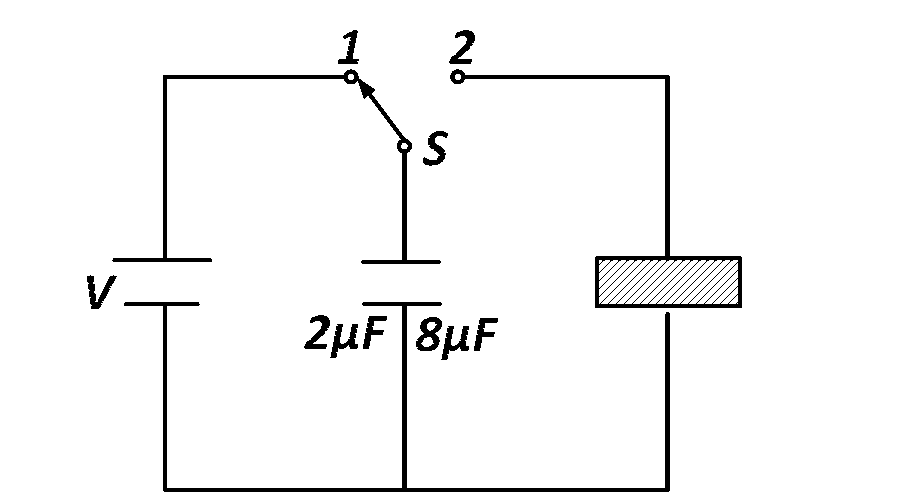
When switch S is connected to terminal 1, the potential difference across the 2 $$\mu$$F capacitor is V volt. Therefore, energy stored in the system is

$${U_1} = {1 \over 2}{C_1}{V^2} = {1 \over 2} \times 2 \times {V^2}$$

$$ = {V^2}\,\mu J$$

When switch S is turned to terminal 2, the charge will flow from 2 $$\mu$$F capacitor to 8 $$\mu$$F capacitor until their potentials are equalized. The common potential is

$${V^2} = {q \over {{C_1} + {C_2}}} = {{{C_1}V} \over {{C_1} + {C_2}}}$$

$$ = {{2V} \over {(2 + 8)}} = {V \over 5}$$ volt

$$\therefore$$ Energy stored in the system now will be

$${U_2} = {1 \over 2}({C_1} + {C_2})V_2^2$$

$$ = {1 \over 2}(2 + 8) \times {\left( {{V \over 5}} \right)^2} = {{{V^2}} \over 5}\mu J$$

$$\therefore$$ Percentage loss of energy is

$${{{U_1} - {U_2}} \over {{U_1}}} \times 100 = {{\left( {{V^2} - {{{V^2}} \over 5}} \right)} \over {{V^2}}} \times 100 = 80\% $$