JEE Advance - Physics (2010 - Paper 2 Offline - No. 9)
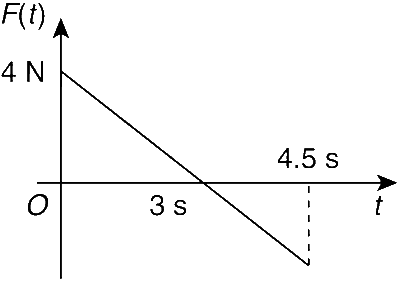
A block of mass 2 kg is free to move along the x-axis. It is at rest and from t = 0 onwards, it is subjected to a time-dependent force F(t) in the x-direction. The force F(t) varies with t as shown in the figure. The kinetic energy of the block after 4.5 s is
4.50 J
7.50 J
5.06 J
14.06 J
Explanation
The t - F diagram is a straight line passing through (0, 4) and (3, 0). The equation of this straight line is
$$F = - {4 \over 3}t + 4$$.
Newton's second law gives acceleration of the block as
$$a = F/m = - {2 \over 3}t + 2$$.
Integrate to get the velocity v at 4.5 s
$$v = \int_0^{4.5} {a\,dt = \int_0^{4.5} {\left( { - {2 \over 3}t + 2} \right)dt = 2.25} } $$ m/s.
Thus, kinetic energy of the block at 4.5 s is
$$K = {1 \over 2}m{v^2} = 5.06$$ J.
Comments (0)


