The forces acting on the oil drop are its weight, buoyant force, and electrostatic force. The buoyant force on the oil drop is very small as compared to other two forces. Thus, the weight of the spherical oil drop is balanced by the electrostatic force

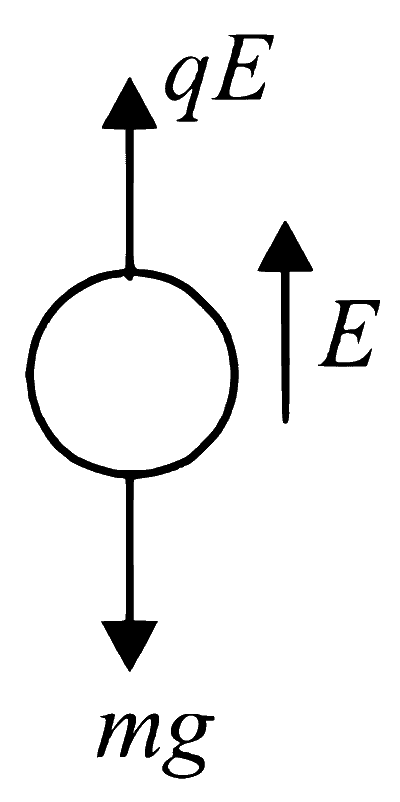
$$qE = mg$$

$$qE = {4 \over 3}\pi {r^3}\rho g$$ ..... (i)

where, r = radius of oil drop, $$\rho$$ = density of oil, q = charge on the oil drop

IN the absence of electric field,

IN equilibrium,

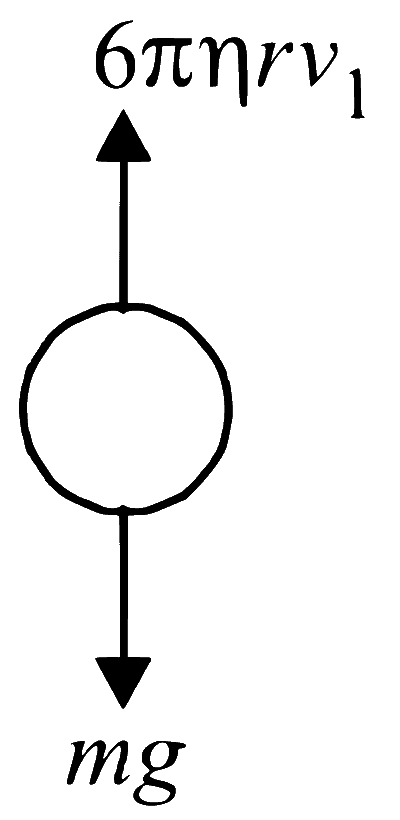
Viscous force on the drop = Weight of the drop

$$6\pi \eta r{v_T} = mg$$

$$6\pi \eta r{v_T} = {4 \over 3}\pi {r^3}\rho g$$ ...... (ii)

where, v_T = terminal velocity, $$\eta $$ = coefficient of viscosity of air

or $${r^2} = {{18 \times \eta \times {v_T}} \over {4 \times \rho \times g}}$$

Substituting the given values, we get

$${r^2} = {{18 \times 1.8 \times {{10}^{ - 5}} \times 2 \times {{10}^{ - 3}}} \over {4 \times 900 \times 9.8}}$$ or $$r = {3 \over 7} \times {10^{ - 5}}$$ m

From equation (i), we get $$q = {{4\pi {r^3}\rho g} \over {3E}}$$

Substituting the given values, we get

$$q = {{4 \times \pi \times {{\left( {{3 \over 7} \times {{10}^{ - 5}}} \right)}^3} \times 900 \times 9.8} \over {3 \times \left( {{{81\pi } \over 7} \times {{10}^5}} \right)}}$$

$$ = {{4 \times \pi \times 7 \times 3 \times 3 \times 3 \times {{10}^{ - 15}} \times 900 \times 9.8} \over {3 \times 81\pi \times {{10}^5} \times 7 \times 7 \times 7}} = 8 \times {10^{ - 19}}C$$