The fundamental mode in a pipe closed at one end and the second harmonic in a string are shown in the figure.

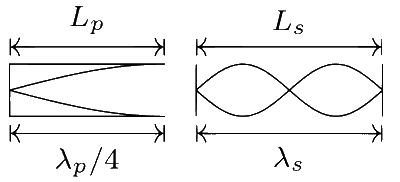
Fundamental frequency of a hollow pipe closed at one end is

$${\upsilon _p} = {v \over {4L}}$$

where, v = speed of sound, L = length of a pipe

Frequency of second harmonic of a string is

$${\upsilon _s} = {2 \over {2l}}\sqrt {{T \over \mu }} = {1 \over l}\sqrt {{T \over \mu }} $$

where, T = tension of the string, m = mass per unit length of the string, l = length of the string

$${\upsilon _s} = {1 \over l}\sqrt {{T \over {{m \over l}}}} = {1 \over l}\sqrt {{{Tl} \over m}} = \sqrt {{T \over {ml}}} $$ ...... (i)

where m is the mass of the string

According to given problem, $${\upsilon _p} = {\upsilon _s}$$

$$\therefore$$ $${v \over {4L}} = \sqrt {{T \over {ml}}} $$ or $$m = {{16{L^2}T} \over {{v^2}l}}$$

Substituting the given values, we get

$$m = {{16 \times {{(0.8)}^2} \times (50)} \over {{{(320)}^2} \times 0.5}} = 0.01$$ kg = 10 gram