JEE Advance - Physics (2010 - Paper 2 Offline - No. 2)
If the radius of the opening of the dropper is $$r$$, the vertical force due to the surface tension on the drop of
radius R (assuming $$r$$ << R) is
$$2\pi rT$$
$$2\pi RT$$
$${{2\pi {r^2}T} \over R}$$
$${{2\pi {R^2}T} \over r}$$
Explanation
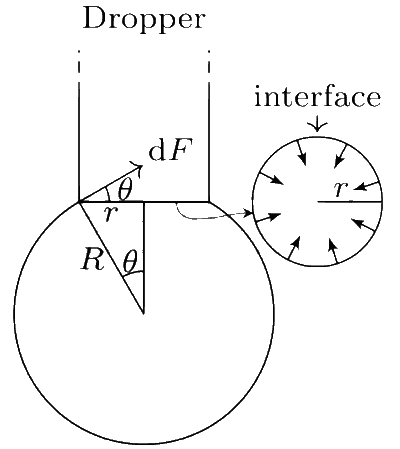
Consider a small element of length dl on the drop-dropper interface. The force on this element is $$dF = T\,dl$$, and it makes an angle $$\theta$$ from the horizontal. Resolve $$dF$$ in the horizontal and the vertical directions to get, $$d{F_h} = T\,dl\cos \theta $$ and $$d{F_v} = T\,dl\sin \theta $$. By symmetry, the force $$d{F_h}$$ on two diametrically opposite elements on circular interface is equal and opposite. Thus, total force in the horizontal direction, $${F_h} = \int {d{F_h} = 0} $$. Integrate the vertical component over the circular interface to get $${F_v} = T(2\pi r)\sin \theta = 2\pi rT(r/R) = 2\pi {r^2}T/R$$.
Comments (0)


