JEE Advance - Physics (2010 - Paper 2 Offline - No. 19)
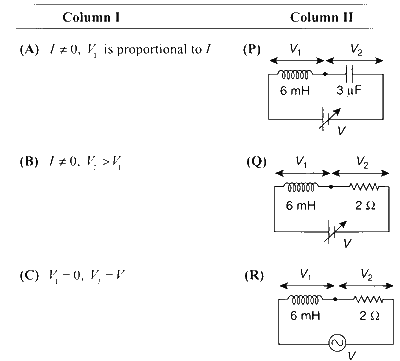
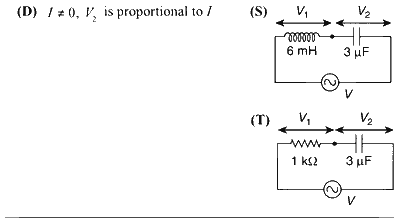
You are given many resistances, capacitors and inductors. These are connected to a variable DC voltage source (the first two circuits) or an AC voltage source of 50 Hz frequency (the next three circuits) in different ways as shown in Column II. When a current I (steady state for DC or rms for AC) flows through the circuit, the corresponding voltage $V_1$ and $V_2$ (indicated in circuits) are related as shown in Column I. Match the two :
Explanation
In circuit $(P)$, under steady state, capacitor will act like an infinite impedance and inductor will act like a zero impedance. Thus, $I=0, V_1=0$, and $V_2=V$.
In circuit $(Q)$, inductor will act as zero resistance in steady state giving us $I=V / R=V / 2, V_1=0$, and $V_2=V$.
In circuit $(R)$, the inductive reactance $X_L$ and impedance $Z$ are
$$ \begin{aligned} X_L & =\omega L=2 \pi \nu L=1.88 \Omega, \quad \text { and } \\\\ Z & =\sqrt{X_L^2+R^2}=2.75 \Omega \end{aligned} $$
Thus, $I=V / Z \neq 0, V_1=X_L I=1.88 I, V_2=R I=2 I$, and $V_2>V_1$.
In circuit (S), inductive reactance $X_L$, capacitive reactance $X_C$, and impedance $Z$ are
$$ \begin{aligned} X_L & =1.88 \Omega \\\\ X_C & =1 /(\omega C)=1061 \Omega, \quad \text { and } \\\\ Z & =X_C-X_L=1059 \Omega \end{aligned} $$
Thus the current in the circuit $I=V / Z \neq 0, V_1=$ $X_L I=1.88 I, V_2=X_C I=1061 I$, and $V_2>V_1$.
In circuit $(T), X_C, R$, and $Z$ are
$$ \begin{aligned} X_C & =1 /(\omega C)=1061 \Omega \\\\ R & =1000 \Omega, \quad \text { and } \\\\ Z & =\sqrt{R^2+X_C^2}=1458 \Omega \end{aligned} $$
Thus, $I=V / Z \neq 0, V_1=R I=1000 I, V_2=X_C I=$ $1061 I$, and $V_2 > V_1$.
Comments (0)


