JEE Advance - Physics (2010 - Paper 2 Offline - No. 18)
Two transparent media of refractive indices $\mu_1$ and $\mu_3$ have a solid lens shaped transparent material of refractive index $\mu_2$ between them as shown in figures in Column II. A ray traversing these media is also shown in the figures. In Column I different relationships between $\mu_1, \mu_2$ and $\mu_3$ are given. Match them to the ray diagram shown in Column II :
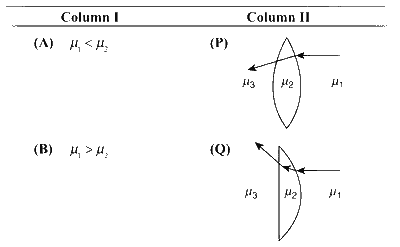
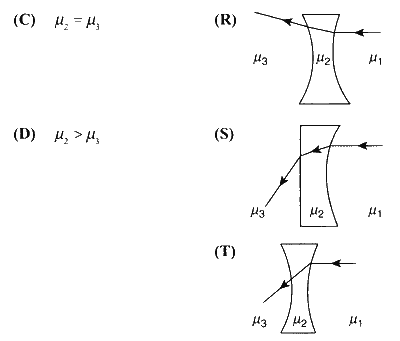
(A)→(P), (R); (B)→(Q), (S), (T); (C)→(P), (R), (T); (D)→(Q), (S)
(A)→(R); (B)→(Q), (S); (C)→(P), (R), (T); (D)→(Q), (S)
(A)→(P), (R); (B)→(S), (T); (C)→(P), (R); (D)→(Q), (S)
(A)→(P); (B)→(Q), (S), (T); (C)→(P), (T); (D)→(Q)
Explanation
If $\mu_1<\mu_2$ then the ray bends towards the normal after refraction at $\mu_1-\mu_2$ interface. Incident rays parallel to the optic axis bend towards the optic axis by the convex lens and away from the optic axis by the concave lens. If $\mu_1>\mu_2$ then the ray bends away from the normal. If $\mu_2=\mu_3$ then the ray goes straight without bending at the $\mu_2-\mu_3$ interface. If $\mu_2>\mu_3$ then the ray bends away from the normal.
Comments (0)


