JEE Advance - Physics (2010 - Paper 2 Offline - No. 14)
At time t = 0, a battery of 10 V is connected across points A and B in the given circuit. If the capacitors have no charge initially, at what time (in seconds) does the voltage across them becomes 4 V? (Take ln5 = 1.6, ln3 = 1.1)
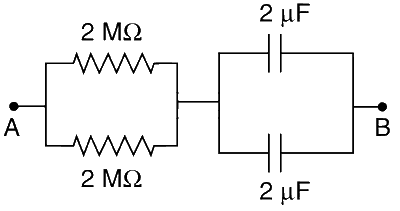
Explanation
The equivalent resistance of the two parallel resistors is
$$R = {{(2\,M\Omega )(2\,M\Omega )} \over {(2\,M\Omega ) + (2\,M\Omega )}} = 1M\Omega $$
The equivalent capacitance of the two parallel capacitors is
$$C = 2\mu F + 2\mu F = 4\mu F$$
This corresponding equivalent diagram is as shown in the figure.
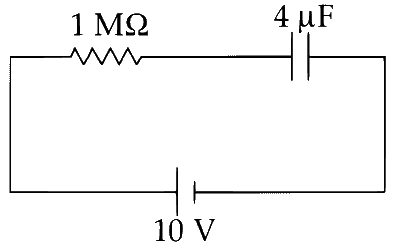
The voltage across the equivalent capacitor is same as the voltage across the individual capacitors (parallel combination). Thus, we need to find time t at which the voltage across C become 4 V in the equivalent circuit (charging of a capacitor). The voltage across C at time t is
$$V = {V_0}\left[ {1 - {e^{ - t/(RC)}}} \right]$$,
which simplifies to
$$t = RC\ln \left( {{{{V_0}} \over {{V_0} - V}}} \right)$$.
Substitute $${V_0} = 10$$ V, $$V = 4$$ V, $$R = 1 \times {10^6}\Omega $$ and $$C = 4 \times {10^{ - 6}}F$$ to get
$$t = 4\ln (5/3) = 4(\ln 5 - \ln 3) = 2\,s$$.
Comments (0)


