JEE Advance - Physics (2010 - Paper 2 Offline - No. 13)
To determine the half-life of a radioactive element, a student plots a graph of $$\ln \left| {{{dN(t)} \over {dt}}} \right|$$ versus t. Here, $${{dN(t)} \over {dt}}$$ is the rate of radioactive decay at time t. If the number of radioactive nuclei of this element decreases by a factor of p after 4.16 years, the value of p is __________.
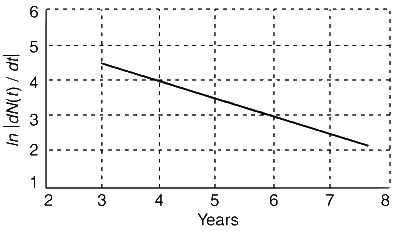
Explanation
The activity of a radioactive substance, having a decay constant $$\lambda$$ and number of nuclei N at time t, is given by
$$A = \left| {dN/dt} \right| = \lambda N = \lambda {N_0}{e^{ - \lambda t}}$$ ..... (1)
Take logarithm on both sides of equation (1) to get
$$\ln \left| {dN/dt} \right| = \ln (\lambda {N_0}) - \lambda t$$ ...... (2)
Thus, the graph between t and $$\left| {dN/dt} \right|$$ is a straight line with slope $$ - \lambda $$.
Slope $$ = - \lambda = {{3 - 4} \over {6 - 4}}$$ (From graph) or $$\lambda = {1 \over 2}$$ year$$-$$1
Half life $${T_{1/2}} = {{0.693} \over \lambda } = 2 \times 0.693$$ years = 1.386 years
4.16 years is approximately 3 half-lives
Nuclei will decay by a factor of 23 = 8
$$\therefore$$ p = 8
Comments (0)


