Let stars A and B are rotating about their centre of mass with angular velocity $$\omega$$.

Let distance of stars A and B from the centre of mass be r_A and r_B respectively as shown in the figure.

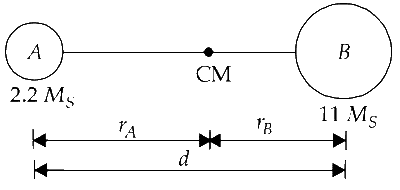
Total angular momentum of the binary stars about the centre of mass is

$$L = {M_A}r_A^2\omega + {M_B}r_B^2\omega $$

Angular momentum of the star B about centre of mass is

$${L_B} = {M_B}r_B^2\omega $$

$$\therefore$$ $${L \over {{L_B}}} = {{({M_A}r_A^2 + {M_B}r_B^2)\omega } \over {{M_B}r_B^2\omega }} = \left( {{{{M_A}} \over {{M_B}}}} \right){\left( {{{{r_A}} \over {{r_B}}}} \right)^2} + 1$$

Since $${M_A}{r_A} = {M_B}{r_B}$$

or, $${{{r_A}} \over {{r_B}}} = {{{M_B}} \over {{M_A}}}$$

$$\therefore$$ $${L \over {{L_B}}} = {{{M_B}} \over {{M_A}}} + 1 = {{11{M_S}} \over {2.2{M_S}}} + 1 = {{11 + 2.2} \over {2.2}} = 6$$