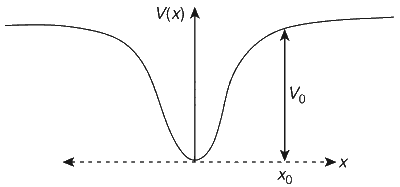
JEE Advance - Physics (2010 - Paper 1 Offline - No. 23)
The acceleration of this particle for $$|x| > {X_0}$$ is
proportional to V0.
proportional to V0/mX0.
proportional to $$\sqrt {{V_0}/m{X_0}} $$.
zero.
Explanation
For $$|x| > {X_0}$$, $$V = {V_0}$$ = constant
Force $$ = - {{dV} \over {dx}} = 0$$
Hence, acceleration of the particle is zero for $$|x| > {X_0}$$.
Comments (0)